算法框架

典型的搜索排序算法框架如下图所示，分为线下训练和线上排序两个部分。模型包括相关性模型、时效性模型、个性化模型和点击模型等。特征包括Query特征、Doc特征、User特征和Query-Doc匹配特征等。日志包括展现日志、点击日志和Query日志。

特征选择

泛特征

Query特征：意图分类、关键词、词权重等。
Doc特征：文章分类、长度、点赞数等。
User特征：年龄、性别等。
Query-Doc匹配特征：类别匹配、BM25。
点击特征：CTR、首次点击等。

日志设计

展现日志：理论上可根据经验进行人工标注打分，并且作为模型的启动训练数据。
点击日志：用户的点击行为日志，可以用于Query日志挖掘，进行查询扩展等，例如多个query搜索结果用户都点击了同一篇文档，则可认为这些query相似。
Query日志：用于和点击／转化数据做联合分析。

模型介绍

相关性模型：Learning to Rank模型

按照样本生成方法和Loss Function不同分为point wise、pair wise和list wise三种，参考L2R算法介绍。2019年Google提出的group wise模型 TF Ranking。
按照模型结构划分，可分为线性排序模型、树模型、深度学习模型，以及组合模型（GBDT+LR，Deep&Wide）。

时效性模型：[待补充]。
个性化模型：逻辑回归(Logistic Regression）。
点击模型：深度置信网络(Deep Belief Networks)。

相关性模型

模型分类

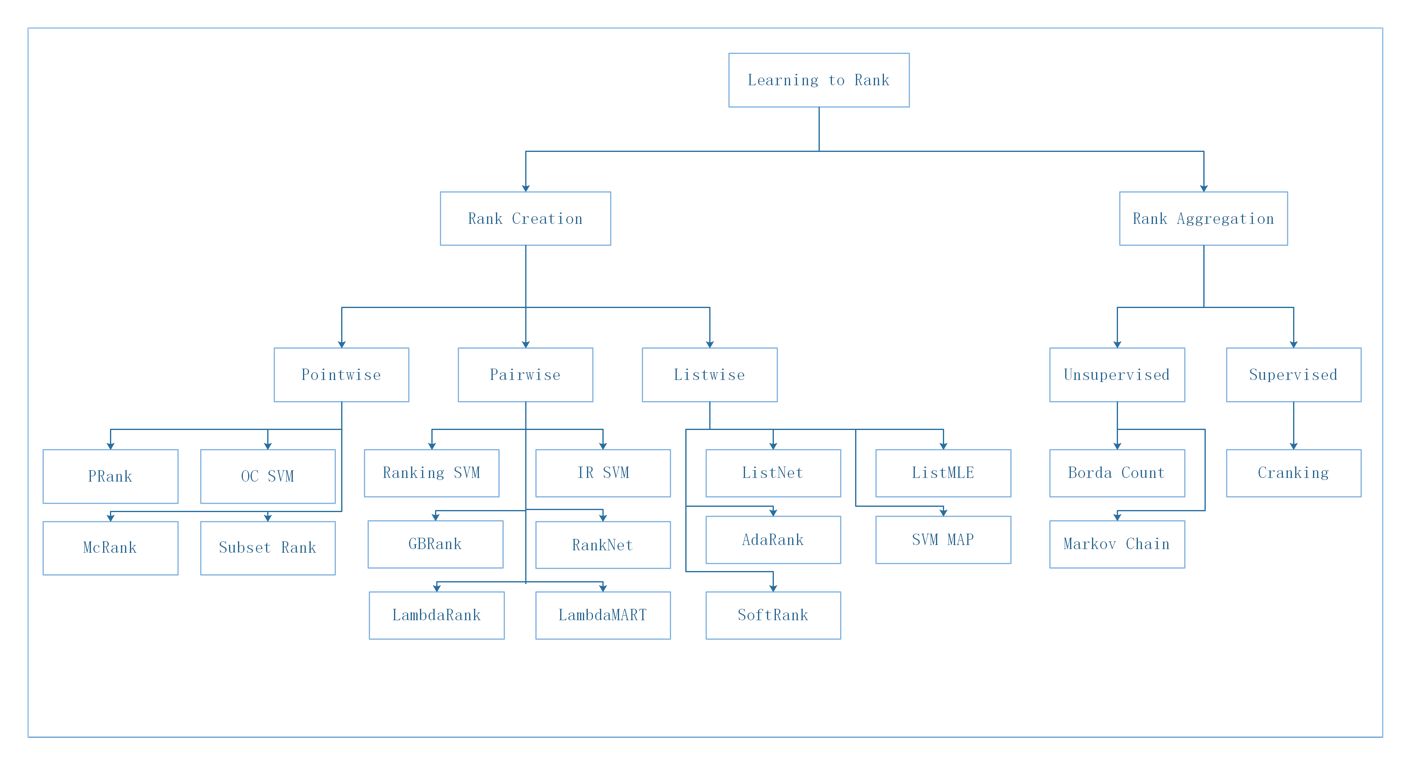
图中Rank Creation指给定查询Query和文档Docs，得到Docs排序结果；Rank Aggregation指综合多个不同的Ranking System的排序结果，得出最终排序结果。

迭代过程

主流模型及评测指标

主流模型对比

模型详情

RankSVM

RankSVM(2003)，将排序问题转化为pairwise的分类问题，然后使用SVM分类模型进行学习并求解，举例说明，两组query及其召回的documents，其中query-doc的相关程度等级分为三档，如下图所示：

同一个query下的不同相关度的doc的feature vector可以进行组合，形成新的feature vector：x1-x2，x1-x3，x2-x3。同时label也会被重新赋值，例如L1-L2，L1-L3，L2-L3。这几个feature vector的label被赋值成分类问题中的positive label。进一步，为了形成一个标准的分类问题，我们还需要有negative samples，这里我们就使用前述的几个新的positive feature vector的反方向向量作为相应的negative samples：x2-x1，x3-x1，x3-x2。另外，需要注意的是，我们在组合形成新的feature vector的时候，不能使用在原始排序问题中处于相同相似度等级的两个feature vector，也不能使用处于不同query下的两个feature vector。

RankNet

微软(2005)提出，属于pairwise算法，从概率的角度来解决排序问题。RankNet的核心是提出了一种概率损失函数来学习Ranking Function，并应用Ranking Function对文档进行排序。这里的Ranking Function可以是任意对参数可微的模型，也就是说，该概率损失函数并不依赖于特定的机器学习模型，在论文中，RankNet是基于神经网络实现的。除此之外，GBDT等模型也可以应用于该框架。
对于任意一个doc对(Ui,Uj)，模型输出的score分别为si和sj，那么根据模型的预测，Ui比Uj与Query更相关的概率为Pij。由于RankNet使用的模型一般为神经网络，根据经验sigmoid函数能提供一个比较好的概率评估。
那么根据模型的预测，Ui比Uj与Query更相关的概率为：
$$\begin{gather*} P_{i j}=P\left(U_{i}>U_{j}\right)=\frac{1}{1+e^{-\sigma\left(s_{i}-s_{j}\right)}} \end{gather*}$$
RankNet证明了如果知道一个待排序文档的排列中相邻两个文档之间的排序概率，则通过推导可以算出每两个文档之间的排序概率。因此对于一个待排序文档序列，只需计算相邻文档之间的排序概率，不需要计算所有pair，减少计算量。
对于训练数据中的Ui和Uj，它们都包含有一个与Query相关性的真实label，比如Ui与Query的相关性label为good，Uj与Query的相关性label为bad，那么显然Ui比Uj更相关。我们定义Ui比Uj更相关的真实概率为Sij：
$$\begin{gather*} \bar{P}_{i j}=\frac{1}{2}\left(1+S_{i j}\right) \end{gather*}$$
如果$U_i$比$U_j$更相关，那么Sij=1；如果$U_i$不如$U_j$相关，那么Sij=−1；如果$U_i$、$U_j$与Query的相关程度相同，那么Sij=0。通常，两个doc的相关度可由人工标注或者从搜索日志中得到。
对于一个排序，RankNet从各个doc的相对关系来评价排序结果的好坏，排序的效果越好，那么有错误相对关系的doc pair就越少。所谓错误的相对关系即如果根据模型输出Ui排在Uj前面，但真实label为Ui的相关性小于Uj，那么就记一个错误pair，RankNet本质上就是以错误的pair最少为优化目标。而在抽象成cost function时，RankNet实际上是引入了概率的思想：不是直接判断Ui排在Uj前面，而是说Ui以一定的概率P排在Uj前面，即是以预测概率与真实概率的差距最小作为优化目标。最后，RankNet使用Cross Entropy作为cost function，来衡量预测相关性概率对真实相关性概率的拟合程度：
$$\begin{gather*} C=-\bar{P}_{i j} \log P_{i j}-\left(1-\bar{P}_{i j}\right) \log \left(1-P_{i j}\right) \end{gather*}$$
该损失函数有以下两个特点：
进一步化简后有：
$$\begin{gather*} \begin{aligned} C_{i j} &=-\frac{1}{2}\left(1+S_{i j}\right) \log \frac{1}{1+e^{-\sigma\left(s_{i}-s_{j}\right)}}-\frac{1}{2}\left(1-S_{i j}\right) \log \frac{e^{-\sigma\left(s_{i}-s_{j}\right)}}{1+e^{-\sigma\left(s_{i}-s_{j}\right)}} \\ &=-\frac{1}{2}\left(1+S_{i j}\right) \log \frac{1}{1+e^{-\sigma\left(s_{i}-s_{j}\right)}}-\frac{1}{2}\left(1-S_{i j}\right)\left[-\sigma\left(s_{i}-s_{j}\right)+\log \frac{1}{1+e^{-\sigma\left(s_{i}-s_{j}\right)}}\right] \\ &=\frac{1}{2}\left(1-S_{i j}\right) \sigma\left(s_{i}-s_{j}\right)+\log \left(1+e^{-\sigma\left(s_{i}-s_{j}\right)}\right) \end{aligned} \end{gather*}$$
当Sij=1，有：
$$\begin{gather*} C=\log \left(1+e^{-\sigma\left(s_{i}-s_{j}\right)}\right) \end{gather*}$$
当Sij=-1，有：
$$\begin{gather*} C=\log \left(1+e^{-\sigma\left(s_{j}-s_{i}\right)}\right) \end{gather*}$$
下图展示了当Sij分别取1，0，-1的时候cost function以si-sj为变量的函数图像：

可以看到当Sij=1时，模型预测的si比sj越大，其代价越小；Sij=−1时，si比sj越小，代价越小；Sij=0时，代价的最小值在si与sj相等处取得。
该损失函数有下面两个特点：

当两个相关性不同的文档算出来的模型分数相同时，损失函数的值大于0，仍会对这对pair做惩罚，使他们的排序位置区分开。
损失函数是一个类线性函数，可以有效减少异常样本数据对模型的影响，因此具有鲁棒性。

代价函数C可微，下面就可以用随机梯度下降法来迭代更新模型参数wk了，即：
$$\begin{gather*} w_{k} \rightarrow w_{k}-\eta \frac{\partial C}{\partial w_{k}} \end{gather*}$$
η为步长，代价C沿负梯度方向变化：
$$\begin{gather*} \Delta C=\sum_{k} \frac{\partial C}{\partial w_{k}} \Delta w_{k}=\sum_{k} \frac{\partial C}{\partial w_{k}}\left(\eta \frac{\partial C}{\partial w_{k}}\right)=-\eta \sum_{k}\left(\frac{\partial C}{\partial w_{k}}\right)^{2}<0 \end{gather*}$$
这表明沿负梯度方向更新参数确实可以降低总代价。
随机梯度下降法时，有：
$$\begin{gather*} \begin{aligned} \frac{\partial C}{\partial w_{k}} &=\frac{\partial C}{\partial s_{i}} \frac{\partial s_{i}}{\partial w_{k}}+\frac{\partial C}{\partial s_{j}} \frac{\partial s_{j}}{\partial w_{k}}=\sigma\left(\frac{1}{2}\left(1-S_{i j}\right)-\frac{1}{1+e^{\sigma\left(s_{i}-s_{j}\right)}}\right)\left(\frac{\partial s_{i}}{\partial w_{k}}-\frac{\partial s_{j}}{\partial w_{k}}\right) \\ &=\lambda_{i j}\left(\frac{\partial s_{i}}{\partial w_{k}}-\frac{\partial s_{j}}{\partial w_{k}}\right) \end{aligned} \end{gather*}$$
其中：
$$\begin{gather*} \lambda_{i j} \equiv \frac{\partial C\left(s_{i}-s_{j}\right)}{\partial s_{i}}=\sigma\left(\frac{1}{2}\left(1-S_{i j}\right)-\frac{1}{1+e^{\sigma\left(s_{i}-s_{j}\right)}}\right) \end{gather*}$$
上面的是对于每一对pair都会进行一次权重的更新，其实是可以对同一个query下的所有文档pair全部带入神经网络进行前向预测，然后计算总差分并进行误差后向反馈，这样将大大减少误差反向传播的次数，加速RankNet训练过程，即利用批处理的梯度下降法：
$$\begin{gather*} \frac{\partial C}{\partial w_{k}}=\sum_{(i, j) \in I}\left(\frac{\partial C_{i j}}{\partial s_{i}} \frac{\partial s_{i}}{\partial w_{k}}+\frac{\partial C_{i j}}{\partial s_{j}} \frac{\partial s_{j}}{\partial w_{k}}\right) \end{gather*}$$
其中：
$$\begin{gather*} \frac{\partial C_{i j}}{\partial s_{i}}=\sigma\left(\frac{1}{2}\left(1-S_{i j}\right)-\frac{1}{1+e^{\sigma\left(s_{i}-s_{j}\right)}}\right)=-\frac{\partial C_{i j}}{\partial s_{j}} \end{gather*}$$
令：
$$\begin{gather*} \lambda_{i j}=\frac{\partial C_{i j}}{\partial s_{i}}=\sigma\left(\frac{1}{2}\left(1-S_{i j}\right)-\frac{1}{1+e^{o\left(s_{i}-s_{j}\right)}}\right) \end{gather*}$$
有：
$$\begin{gather*} \begin{aligned} \frac{\partial C}{\partial w_{k}} &=\sum_{(i, j) \in I} \sigma\left(\frac{1}{2}\left(1-S_{i j}\right)-\frac{1}{1+e^{\sigma\left(s_{i}-s_{j}\right)}}\right)\left(\frac{\partial s_{i}}{\partial w_{k}}-\frac{\partial s_{j}}{\partial w_{k}}\right) \\ &=\sum_{(i, j) \in I} \lambda_{i j}\left(\frac{\partial s_{i}}{\partial w_{k}}-\frac{\partial s_{j}}{\partial w_{k}}\right) \\ &=\sum_{i} \lambda_{i} \frac{\partial s_{i}}{\partial w_{k}} \end{aligned} \end{gather*}$$

如何理解上式最后一步的化简及λi的意义呢？前面讲过集合I中只包含label不同的doc的集合，且每个pair仅包含一次，即(Ui,Uj)与(Uj,Ui)等价。为方便起见，我们假设I中只包含Ui相关性大于Uj的pair(Ui,Uj)，即I中的pair均满足Sij=1，那么：
$$\begin{gather*} \lambda_{i}=\sum_{j:(i, j) \in I} \lambda_{i j}-\sum_{k:(k, i) \in I} \lambda_{k i} \end{gather*}$$
举例说明，假设有三个doc，其真实相关性满足U1>U2>U3，那么集合I中就包含{(1,2), (1,3), (2,3)}共三个pair，则：
$$\begin{gather*} \frac{\partial C}{\partial w_{k}}=\left(\lambda_{12} \frac{\partial s_{1}}{\partial w_{k}}-\lambda_{12} \frac{\partial s_{2}}{\partial w_{k}}\right)+\left(\lambda_{13} \frac{\partial s_{1}}{\partial w_{k}}-\lambda_{13} \frac{\partial s_{3}}{\partial w_{k}}\right)+\left(\lambda_{23} \frac{\partial s_{2}}{\partial w_{k}}-\lambda_{23} \frac{\partial s_{3}}{\partial w_{k}}\right) \end{gather*}$$
显然λ1=λ12+λ13，λ2=λ23−λ12，λ3=−λ13−λ23。
λi决定着第i个doc在迭代中的移动方向和幅度，真实的排在Ui前面的doc越少，排在Ui后面的doc越多，那么文档Ui向前移动的幅度就越大。
如何理解呢？我们可以结合损失函数C的图像来看，第i个doc与query越相关，λi越大，则wk变化越大，损失函数C减少越多，而损失函数C的图像在Sij=1时越小，si-sj越大，表明模型输出的文档i的分数与文档j分数相差越大，即文档Ui向前移动的幅度就越大。

GBrank

基本思想：对两个具有relative relevance judgment的Documents，利用pairwise的方式构造一个特殊的 loss function，再使用GBDT的方法来对此loss function进行优化，求解其极小值。
GBRank的创新点之一就在于构造一个特殊的loss function。首先，我们需要构造pair，即在同一个query下有两个doc，可以通过人工标注或者搜索日志来对这两个doc与该query的相关程度进行判断，得到一个pair关系，即其中一个doc的相关程度要比另一个doc的相关程度更高，这就是relative relevance judgment。一旦我们有了这个pairwise的相对关系，问题就成了如何利用这些doc pair学习出一个排序模型。
假设我们有以下的preference pairs 作为training data：
$$\begin{gather*} \left\{\left(x_{i}^{(1)}, x_{i}^{(2)}\right), x_{i}^{(1)}>x_{i}^{(2)}\right\}_{i=1}^{N} \end{gather*}$$
则可构造损失函数L(f)，与SVM中hinge loss类似:
$$\begin{gather*} L(f)=\frac{1}{2} \sum_{i=1}^{N}\left(\max \left\{0, \tau-\left(f\left(x_{i}^{(1)}\right)-f\left(x_{i}^{(2)}\right)\right\}\right)^{2}\right. \end{gather*}$$
在hinge loss的基础上，将原来为1的参数改成了τ。即当两个doc相关度差距达到τ以上的时候，loss才为0。若f(x)输出固定，那么损失函数最少，但不是训练目标。
然后问题就变成了怎样对这个loss function进行优化求解极小值。这里使用了GBDT的思想，即Functional Gradient Descent的方法。

在GBDT中，Functional Gradient Descent的使用为：将需要求解的f(x)表示成一个additive model，即将一个函数分解为若干个小函数的加和形式，而这每个小函数的产生过程是串行生成的，即每个小函数都是在拟合loss function在已有的f(x)上的梯度方向（由于训练数据是有限个数的，所以f(x)是离散值的向量，而此梯度方向也表示成一个离散值的向量），然后将拟合的结果函数进一步更新到f(x)中，形成一个新的f(x)。

对于loss function，利用Functional Gradient Descent的方法优化为极小值的过程为：将f(x)表示成additive model，每次迭代的时候，用一个regression tree来拟合loss function在当前f(x)上的梯度方向。此时由于训练数据是有限个数的，f(x)同样只是一系列离散值，梯度向量也是一系列离散值，则可使用regression tree来拟合这一系列离散值。
但不同之处在于，由于使用pairwise方法，这里的loss function中，有两个不一样的f(x)的离散值，所以每次我们需要对f(x)在这两个点上的值都进行更新，即需要对一个training instance计算两个梯度方向。首先将以下两个变量看作未知变量：
$$\begin{gather*} f\left(x_{i}^{(1)}\right), \quad f\left(x_{i}^{(2)}\right), \quad i=1, \cdots, N \end{gather*}$$
然后求解loss function对这两个未知变量的梯度（分别对两个未知变量求导），如下：
$$\begin{gather*} -\max \left\{0, f\left(x_{i}^{(2)}\right)-f\left(x_{i}^{(1)}\right)+\tau\right\}, \quad \max \left\{0, f\left(x_{i}^{(2)}\right)-f\left(x_{i}^{(1)}\right)+\tau\right\}, \quad i=1, \cdots, N \end{gather*}$$
如果$f\left(x_{i}^{(1)}\right)-f\left(x_{i}^{(2)}\right) \geq \tau$，则此时对应的loss为0，我们无需对f(x)进行迭代更新；如果f\left(x_{i}^{(1)}\right)-f\left(x_{i}^{(2)}\right)<\tauloss不为0，我们需要对f(x)进行迭代更新，即使得新的f(x)在这个instance上的两个点的预测值能够更接近真实值。f(x)更新类似于梯度下降方法中参数的更新：
$$\begin{gather*} f_{k}(x)=f_{k-1}(x)-\eta \nabla L\left(f_{k}(x)\right) \end{gather*}$$
pairwise方法中，具体为：
$$\begin{gather*} \begin{aligned} &f_{k}\left(x_{i}^{(1)}\right)=f_{k-1}\left(x_{i}^{(1)}\right)+\eta\left(f_{k-1}\left(x_{i}^{(2)}\right)-f_{k-1}\left(x_{i}^{(1)}\right)+\tau\right)\\ &f_{k}\left(x_{i}^{(2)}\right)=f_{k-1}\left(x_{i}^{(2)}\right)-\eta\left(f_{k-1}\left(x_{i}^{(2)}\right)-f_{k-1}\left(x_{i}^{(1)}\right)+\tau\right) \end{aligned} \end{gather*}$$
当学习速率η等于1的时候，更新公式即为：
$$\begin{gather*} \begin{aligned} &f_{k}\left(x_{i}^{(1)}\right)=f_{k-1}\left(x_{i}^{(2)}\right)+\tau\\ &f_{k}\left(x_{i}^{(2)}\right)=f_{k-1}\left(x_{i}^{(1)}\right)-\tau \end{aligned} \end{gather*}$$
当我们收集到所有loss值不为0的training instance后，我们便得到了其对应的更新值：
$$\begin{gather*} \left\{\left(x_{i}^{(1)}, f_{k-1}\left(x_{i}^{(2)}\right)+\tau\right),\left(x_{i}^{(2)}, f_{k-1}\left(x_{i}^{(1)}\right)-\tau\right)\right\} \end{gather*}$$
接着，使用一棵regression tree对这些数据进行拟合，生成一个拟合函数$g_{k}(x)$，然后将这次迭代更新的拟合函数更新到f(x)中，此处采用线性叠加的方式：
$$\begin{gather*} f_{k}(x)=\frac{k f_{k-1}(x)+\beta g_{k}(x)}{k+1} \end{gather*}$$
其中，ß为shrinking系数。
为什么在每次迭代更新的时候，新的regression tree不像GBDT中那样，纯粹地去拟合梯度方向（一个离散值的向量），而是去拟合：
$$\begin{gather*} f_{k}(x)=f_{k-1}(x)-\eta \nabla L\left(f_{k}(x)\right) \end{gather*}$$
这样一个原始预测值+梯度更新值后的新预测值向量呢？
因为在每次迭代更新的时候，只是取了部分训练数据（即所有loss值不为0的training instance中的doc pair），所以每次拟合的时候，都只是对这部分数据进行训练，得到一个regression tree，然后把这个新的拟合函数（即regression tree）添加到总的预测函数f(x)中去，即这个regression tree在预测时候是需要对所有训练数据，而不是部分数据，进行预测的。所以如果每次迭代是去拟合梯度的话（梯度方向完全有可能与当前的f(x)向量方向相差很大），在预测的时候，这个regression tree对其余数据（并没有参与这个regression tree训练的数据）的预测值会偏离它们原始值较多，而且这个偏离是不在期望之中的，因为这些数据的当前预测值已经相对靠谱了（不会对loss function有贡献）。所以，当每次拟合的目标是原始f(x)向量 + 梯度向量的时候，这个新的向量不会跑的太偏（即跟原始向量相差较小），这时候拟合出来的结果regression tree在对整体数据进行预测的时候，也不会跑的太偏，只是会根据梯度方向稍微有所改变，对其它并不需要更新的数据的影响也相对较小。但同时也在逐渐朝着整体的优化方向上去尝试，所以才会这么去做。（以一个队伍在山峰间移动，分别寻找各自合适位置为例）。

LambdaRank

RankNet以错误pair最少为优化目标的RankNet算法，然而许多时候仅以错误pair数来评价排序的好坏是不够的，像NDCG或者ERR等评价指标就只关注top k个结果的排序，当我们采用RankNet算法时，往往无法以这些指标为优化目标进行迭代，所以RankNet的优化目标和IR评价指标之间还是存在gap的，如下图所示：

如上图所示，每个线条表示文档，蓝色表示相关文档，灰色表示不相关文档，RankNet以pairwise error的方式计算cost，左图的cost为13，右图通过把第一个相关文档下调3个位置，第二个文档上条5个位置，将cost降为11，但是像NDCG或者ERR等评价指标只关注top k个结果的排序，在优化过程中下调前面相关文档的位置不是我们想要得到的结果。图 1右图左边黑色的箭头表示RankNet下一轮的调序方向和强度，但我们真正需要的是右边红色箭头代表的方向和强度，即更关注靠前位置的相关文档的排序位置的提升。LambdaRank正是基于这个思想演化而来，其中Lambda指的就是红色箭头，代表下一次迭代优化的方向和强度，也就是梯度。
LambdaRank在RankNet的加速算法形式的基础上引入评价指标Z （如NDCG、ERR等），把交换两个文档的位置引起的评价指标的变化|ΔNDCG|，作为其中一个因子，实验表明对模型效果有显著的提升：
$$\begin{gather*} \lambda_{i j}=\frac{\partial C\left(s_{i}-s_{j}\right)}{\partial s_{i}}=\frac{-\sigma}{1+e^{\sigma\left(s_{i}-s_{j}\right)}}\left|\Delta_{N D C G}\right| \end{gather*}$$
ΔNDCG表示将Ui和Uj进行交换，交换后排序的NDCG与交换前排序的NDCG的差值。
损失函数的梯度代表了文档下一次迭代优化的方向和强度，由于引入了IR评价指标，Lambda梯度更关注位置靠前的优质文档的排序位置的提升。有效的避免了下调位置靠前优质文档的位置这种情况的发生。LambdaRank相比RankNet的优势在于分解因式后训练速度变快，同时考虑了评价指标，直接对问题求解，效果更明显。

LambdaMART

Mart（Multiple Additive Regression Tree，Mart就是GBDT），定义了一个框架，缺少一个梯度。
LambdaRank重新定义了梯度，赋予了梯度新的物理意义。

因此，所有可以使用梯度下降法求解的模型都可以使用这个梯度，MART就是其中一种，将梯度Lambda和MART结合就是大名鼎鼎的LambdaMART。
MART的原理是直接在函数空间对函数进行求解，模型结果由许多棵树组成，每棵树的拟合目标是损失函数的梯度，在LambdaMART中就是Lambda。LambdaMART的具体算法过程如下：

可以看出LambdaMART的框架其实就是MART，主要的创新在于中间计算的梯度使用的是Lambda，是pairwise的。MART需要设置的参数包括：树的数量M、叶子节点数L和学习率v，这3个参数可以通过验证集调节获取最优参数。

MART输出值的计算：

首先设置每棵树的最大叶子数，基分类器通过最小平方损失进行分裂，达到最大叶子数量时停止分裂
使用牛顿法得到叶子的输出，计算效用函数对模型得分的二阶导$\frac{\partial \lambda_{i}}{\partial s_{i}}=\frac{\partial^{2} C}{\partial^{2} s_{i}}$
$$\begin{gather*} \frac{\partial^{2} C}{\partial^{2} s_{i}}=\sum_{\{i, j\} \rightleftharpoons I} \sigma^{2}\left|\triangle Z_{i j}\right| \rho_{i j}\left(1-\rho_{i j}\right) \end{gather*}$$
得到第m颗树的第k个叶子的输出值:
$$\begin{gather*} \gamma_{k m}=\frac{\sum_{x_{i} \in R_{k m}} \frac{\partial C}{\partial s_{i}}}{\sum_{x_{i} \in R_{k m}} \frac{\partial^{2} C}{\partial^{2} s_{i}}}=\frac{-\sum_{x_{i} \in R_{k m}} \sum_{\{i, j\} \rightleftharpoons I}\left|\triangle Z_{i j}\right| \rho_{i j}}{\sum_{x_{i} \in R_{k m}} \sum_{\{i, j\} \rightleftharpoons I}\left|\Delta Z_{i j}\right| \sigma \rho_{i j}\left(1-\rho_{i j}\right)} \end{gather*}$$
$x_i$为第i个样本，$x_{i} \in R_{k m}$意味着落入该叶子的样本，这些样本共同决定了该叶子的输出值。

LambdaMART具有很多优势：

适用于排序场景：不是传统的通过分类或者回归的方法求解排序问题，而是直接求解;
损失函数可导：通过损失函数的转换，将类似于NDCG这种无法求导的IR评价指标转换成可以求导的函数，并且赋予了梯度的实际物理意义，数学解释非常漂亮;
增量学习：由于每次训练可以在已有的模型上继续训练，因此适合于增量学习;
组合特征：因为采用树模型，因此可以学到不同特征组合情况;
特征选择：因为是基于MART模型，因此也具有MART的优势，可以学到每个特征的重要性，可以做特征选择;
适用于正负样本比例失衡的数据：因为模型的训练对象具有不同label的文档pair，而不是预测每个文档的label，因此对正负样本比例失衡不敏感。

LambdaMART是不是很好懂？

有较多博客、资料在此戛然而止，好像上述资料已经足够理解LambdaMART了，这也让我一度怀疑自己的IQ，基础和我一样不太好的兄弟们可以进入另一篇博客，我们从提升树、梯度提升树和梯度提升决策树说起，并结合Ranklib源码和具体的例子，以及微软的相关技术报告一起来看看LambdaMART的真相。

爱奇艺实践：
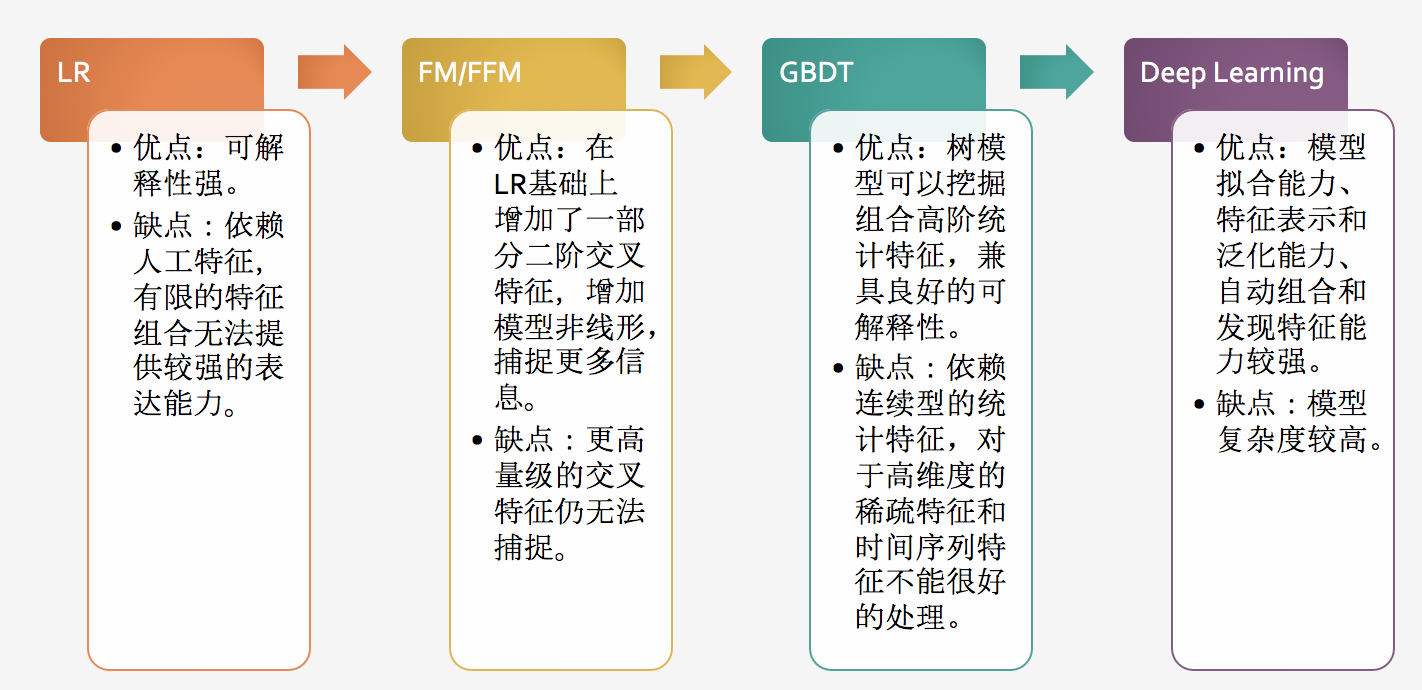
在没有加入稀疏类特征之前，我们的模型是LambdaMART模型，在IR领域是最先进的模型，该模型是一个gbdt模型，基于boosting思想，不断增加决策树，来减小残差。该模型在很多竞赛中表现良好，因为不用过多的特征处理，树模型会考虑特征本身的数据分布，同时有很好的学习泛化能力，树结构很难兼容高维稀疏特征，比方说我们的document是上亿级的特征，很难每个节点走一次树的分割，所以对于加入稀疏特征的时候，树模型会遇到瓶颈。但是在处理高维稀疏特征的时候，像LR、FM、FFM可以认为是线性模型，特征的增加并不会对此类模型造成压力，上亿维也没关系。LR模型弱点在于特征组合能力不足，很多情况下特征组合方式比较重要，树模型从根节点到叶子节点的路径其实是一种组合方式。如下图所示：

深度模型

DNN

爱奇艺实现：

底层是query和document的描述文本做多粒度切词，之后做embedding后加权平均，得到document和query的向量表达，拼接这两组向量，同时再做点积，（两个向量越来越相近，拼接的时候希望上层网络学到两个向量的相似性，需要有足够的样本和正负样例，所以我们自己做了点积）。除了向量特征，模型也适用了稠密特征，即利用gbdt抽取特征，与embedding特征做拼接，最后经过三个全连接层，接sigmoid函数，就可以得到样本的score，并在此基础上用ndcg的衡量标准去计算损失，从而反向优化网络结构。而在online服务侧，则直接用样本去predict得分。这个模型上线之后，效果非常明显。其中，二次搜索率降低（二次搜索率越低越好，说明用户一次搜中）。

Wide&Deep

美团点评模型框架：

美团点评模型具体实现：

在训练时，分别对样本数据进行清洗和提权。在特征方面，对于连续特征，用Min-Max方法做归一化。在交叉特征方面，结合业务需求，提炼出多个在业务场景意义比较重大的交叉特征。用Adam做为优化器，用Cross Entropy做为损失函数。在训练期间，与Wide & Deep Learning论文中不同之处在于，将组合特征作为输入层分别输入到对应的Deep组件和Wide组件中。然后在Deep部分将全部输入数据送到3个ReLU层，在最后通过Sigmoid层进行打分。训练数据7000万+，并用超过3000万的测试数据进行线下模型预估。Batch－Size设为50000，Epoch设为20。
线上AB实验结果：

LambdaDNN

大众点评搜索排序模型，基于TensorFlow分布式框架实现。

NDCG的计算公式中，折损的权重是随着位置呈指数变化的。然而实际曝光点击率随位置变化的曲线与NDCG的理论折损值存在着较大的差异。
对于移动端的场景来说，用户在下拉滑动列表进行浏览时，视觉的焦点会随着滑屏、翻页而发生变动。例如用户翻到第二页时，往往会重新聚焦，因此，会发现第二页头部的曝光点击率实际上是高于第一页尾部位置的。我们尝试了两种方案去微调NDCG中的指数位置折损：
根据实际曝光点击率拟合折损曲线：根据实际统计到的曝光点击率数据，拟合公式替代NDCG中的指数折损公式，绘制的曲线如图12所示。
计算Position Bias作为位置折损：Position Bias在业界有较多的讨论，用户点击商户的过程可以分为观察和点击两个步骤：a.用户需要首先看到该商户，而看到商户的概率取决于所在的位置；b.看到商户后点击商户的概率只与商户的相关性有关。步骤a计算的概率即为Position Bias，这块内容可以讨论的东西很多，这里不再详述。

经过上述对NDCG计算改造训练出的LambdaDNN模型，相较Base树模型和Pointwise DNN模型，在业务指标上有了非常显著的提升。

LambdaDCN

Lambda梯度除了与DNN网络相结合外，也可以与绝大部分常见的网络结构相结合。为了进一步学习到更多交叉特征，美团点评团队在LambdaDNN的基础上分别尝试了LambdaDeepFM和LambdaDCN网络；其中DCN网络是一种加入Cross的并行网络结构，交叉的网络每一层的输出特征与第一层的原始输入特征进行显性的两两交叉，相当于每一层学习特征交叉的映射去拟合层之间的残差。

离线的对比实验表明，Lambda梯度与DCN网络结合之后充分发挥了DCN网络的特点，简洁的多项式交叉设计有效地提升模型的训练效果。NDCG指标对比效果如下图所示：

补充模型

FM

DSSM

点击模型

DBN模型

IRGAN

模型选择

LambdaRank
LambdaMART
Wide&Deep

模型组合

爱奇艺实践：

针对GBDT和LR模型的优缺点，做了进一步的模型组合的尝试：
第一种方式，用 LR 模型把高维稠密特征进行学习，学习出高维特征，把该特征和原始特征做拼接，学习 gbdt 模型。
该办法效果不好，提升很弱。
剖析缘由： 把高维特征刚在一个特征去表达，丢掉了原始的特征。
第二种方式，用 gbdt 去学，学习后把样本落入叶子节点信息来进来与高维稠密特征拼接，在此根底上用 LR 学习。
该模型效果变差。
剖析缘由： 点击类和穿插类特征是对排序影响最大的特征，这类特征和大量的稠密类特征做拼接时，重要性被稀释了，导致模型的学习能力变弱。

工程实现

Python训练+Golang部署

LambdaRank，基于xgboost实现，参考：https://github.com/dmlc/xgboost/tree/master/demo/rank
LambdaMART，基于LightGBM实现，参考：https://github.com/jiangnanboy/learning_to_rank
Wide&Deep基于TensorFlow实现，参考：https://github.com/tensorflow/ranking

[待进一步整理]