前言
本篇论文获得SIGIR 2020 Best Paper,旨在通过构建公平的无偏统计量,解决动态排序中的不公平问题。排序算法广泛应用于推荐和搜索场景,但目前的算法大多存在马太效应,例如热搜场景,排名越靠前被点击的概率也就越大,在一段时间内,越是靠前的文章就越会被人点击,然后其排名持续提升,而初始排在后面的文章由于没有得到公平曝光而逐渐无人问津。不过仅仅考虑热搜场景的话,这里的马太效应是符合要求的,但在其他排序场景中,就会存在一些问题,例如在购物场景下,初始排名靠后的商品由于无法得到充分曝光相对成交量很少,这对商家来说是难以接受的。
曝光模型偏差
以新闻网站动态排序文章为例,假设有六篇文章,且没有关于排名的信息,那么我们可能向第一个用户提供随机的排名。根据该用户的点击行为更新排名,类似的,根据后续的用户点击行为,持续更新排名。最后找到一个适合大多数用户的排名,如下图所示: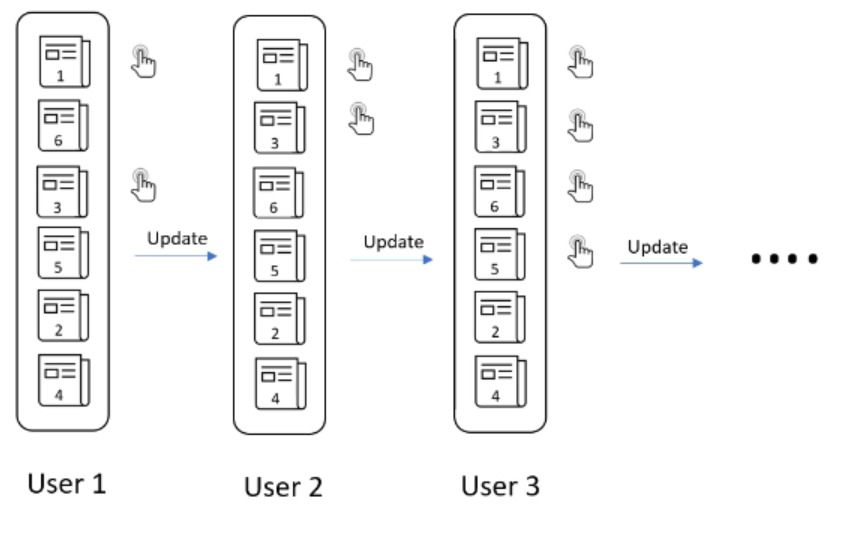
这种动态学习排序的方式存在两个问题:
- 位置选择偏差。每篇文章的平均点击次数并不等于喜欢这篇文章用户数,因为位置越靠后,获得的用户注意力就越少,点击次数相应较少,如下图所示:
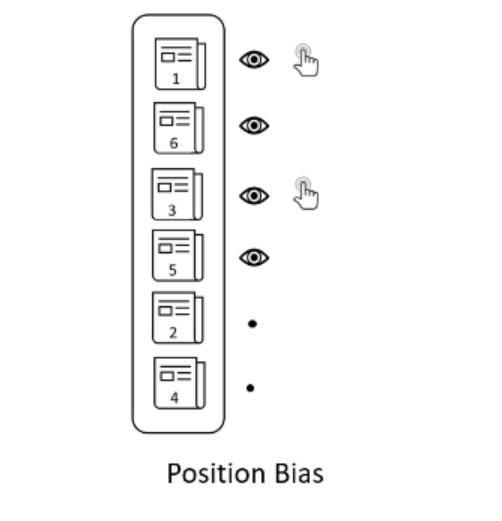
这是一个“富者越富”的问题,上图中的文章4上升到顶部的机会显然低于从一开始就在顶部的文章。
曝光分配不均。假设我们能够以某种方式计算出文章的真实相关性,仍然会存在问题。假设上文中提到的六篇文章属于$G_{Left}$和$G_{Right}$两组,即有两组用户分别喜欢对应的文章,如下图所示:
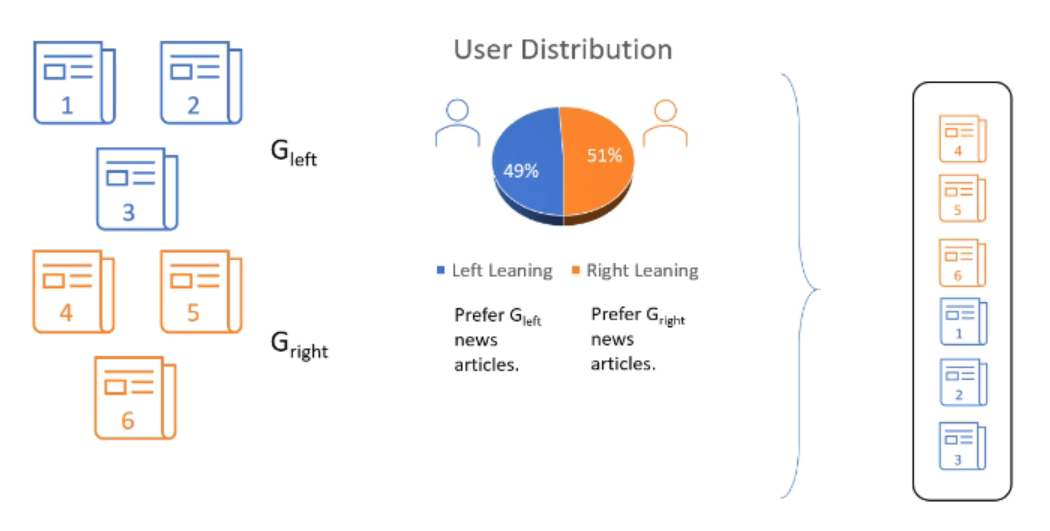
根据排序规则,由于喜欢Right组文章的用户更多,因此会把Right组的文章全部排在前面,这导致Left组文章无法得到公平曝光,而相应的Left组用户也开始不喜欢这个产品,导致用户流失。但喜欢两个组文章的用户数只有2%的差异,这显然是不合理的。
那么公平的动态排序算法要具有两个性质:
- 无偏性。用来描述用户偏好的统计量是无偏的。
- 公平性。算法可以根据相关性对曝光量进行公平的分配。
文章排序模型
仍以文章排序模型为例,该模型存在Exposure Unfairness和Impact Unfairness,如下图所示:

曝光
为保证文章得到公平曝光,我们希望单位相关度下的期望曝光是一致的,即曝光可以表示为相关度的函数:
$$\begin{gather*} \operatorname{Exp}(G \mid x)=f(\operatorname{Rel}(G \mid x)) \end{gather*}$$从公平的角度,我们希望各组文章进行与其相关度成比例的曝光:
$$\begin{gather*} \frac{\operatorname{Exp}\left(G_{0} \mid x\right)}{\operatorname{Exp}\left(G_{1} \mid x\right)}=\frac{\operatorname{Rel}\left(G_{0} \mid x\right)}{\operatorname{Rel}\left(G_{1} \mid x\right)} \end{gather*}$$那么公平性的差异就是两组单位相关度曝光的差异:
$$\begin{gather*} \begin{array}{l} D^{E}\left(G_{0}, G_{1}\right) \\ =\left|\frac{E x p\left(G_{0} \mid x\right)}{\operatorname{Rel}\left(G_{0} \mid x\right)}-\frac{\operatorname{Exp}\left(G_{1} \mid x\right)}{\operatorname{Rel}\left(G_{1} \mid x\right)}\right| \end{array} \end{gather*}$$影响力
类似于曝光,影响力也是相关度的函数,这里的影响力可以认为是预期点击率:
$$\begin{gather*} \operatorname{Imp}(G \mid x)=f(\operatorname{Rel}(G \mid x)) \end{gather*}$$同样,影响力的差异定义为单位相关度的影响力:
$$\begin{gather*} D^{I}\left(G_{0}, G_{1}\right)=\left|\frac{\operatorname{Imp}\left(G_{0} \mid x\right)}{\operatorname{Rel}\left(G_{0} \mid x\right)}-\frac{\operatorname{Imp}\left(G_{1} \mid x\right)}{\operatorname{Rel}\left(G_{1} \mid x\right)}\right| \end{gather*}$$仍以文章排序为例,不妨设$\text { Exposure }(j)=1 / \log (1+j)$,如下图所示,可以看到两个组仅仅2%的差异导致曝光和影响力均不公平。
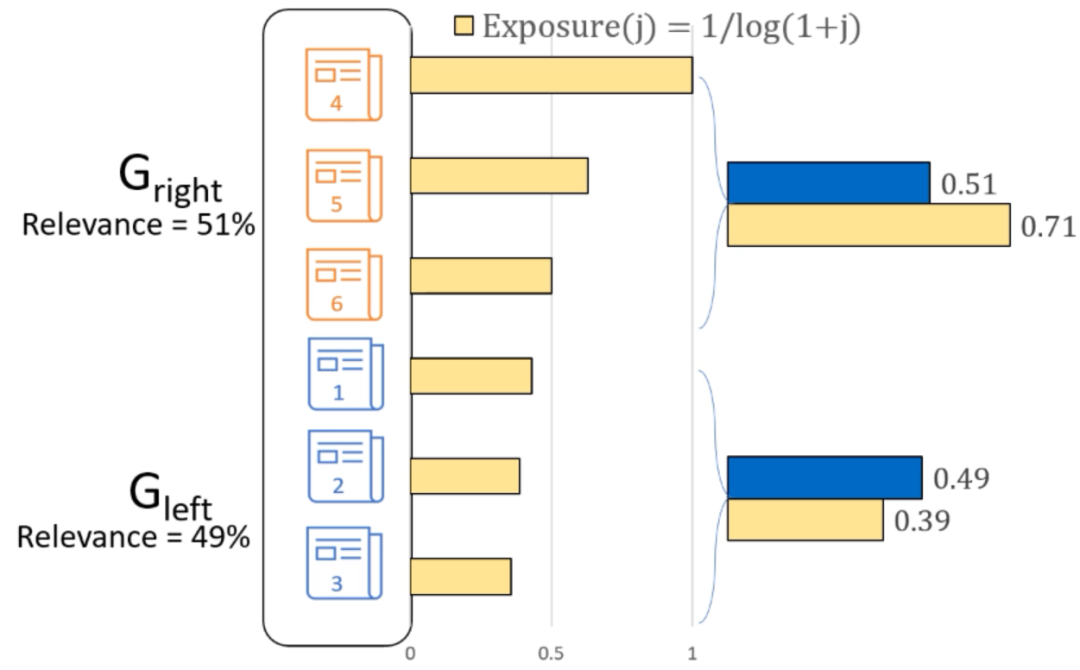
动态排序
假设给定一批文章,x表示用户信息,r表示文章与用户的相关性,t表示时间,则特定时间用户信息表示为$x_{t}$,特定时间相关性表示为$r_{t}$,一般来说,$x_{t}$是明确已知的,$r_{t}$是隐性不可知的。现有一个排序规则$π_{t}$可以得到排序打分$δ_{t}$,则利用这个排序方法可以获得用户的反馈$c_{t}(d)$,例如可以用0和1表示是否点击,掌握用户的反馈后可以利用动态排序算法得到t+1时刻的排序规则$π_{t+1}$。
$c_{t}(d)$用于描述用户的偏好,如果以点击和未点击来判断的话,用户偏好与相关性的关系可以表示为:$$\begin{gather*} c_{t}(d)=\left\{\begin{array}{rr} r_{t}(d), & \text { if } e_{t}(d)=1 \\ 0, & \text { otherwise } \end{array}\right. \end{gather*}$$ $e_{t}$表示该文章是否曝光(有机会经过用户偏好试探),当且仅当文章被曝光且被点击时,用户的偏好才能被记录。也就是说,$c_{t}(d)$只能表达经过试探的文章的偏好,对于未经试探的文章,无法正确记录其偏好。因为当$c_{t}(d)=0$时,无法判断是因为未曝光还是因为曝光但没有点击导致的0。随着时间推移,迭代轮数增多,这个错误会更加明显。
$e_{t}$也有问题,对于新的文章,由于无法知道用户对其偏好,因此要通过试探的方法获得。那么如何确定文章的曝光顺序呢?一般来说会按排序分数确定曝光位置,排在越前面,被曝光的概率就越大,即用排序打分来决定文章的曝光,也就是position bias:
$c_{t}(d)$用于描述用户的偏好,如果以点击和未点击来判断的话,用户偏好与相关性的关系可以表示为:
$$\begin{gather*} e_{t}(d)=\sigma_{d} \end{gather*}$$ $\sigma_{t}$可以理解为排序的打分,例如预估CTR,由用户信息、文章和两者的相关性计算得到。假设不进行动态调整,那么排序逻辑可以表示为:
$$\begin{gather*} \pi(x)=\operatorname{argsort}_{d \in D}[R(d \mid x)] \end{gather*}$$
根据用户X的特征计算用户与文章d的相关度,进而根据打分公式获得排序分数,决定展示给特定用户的顺序。相关度$R(d|x)$也可以简化为$R(d)$,即大部分用户对该文章的偏好,不考虑用户个性化偏好。如果要进行动态调整,那么$R(d|x)$需要根据时间进行调整,其调整的依据就是$c_{t}(d)$用户偏好。
具体建模
下面我们看一下论文中描述公平性和无偏性的方式:
公平性
关注是否曝光和用户偏好两个变量。
是否曝光与排序打分、用户信息和相关性有关,其概率表示为:
$$\begin{gather*} p_{t}(d)=P\left(e_{t}(d)=1 \mid \sigma_{t}, x_{t}, r_{t}\right) \end{gather*}$$论文中将单个物料扩展为一组物料,使用组内所有物料的平均曝光度,其中$G_i$表示第i组的物料。
对物料的偏好可以使用R(d)衡量,同样使用组内所有物料偏好的平均值:
$$\begin{gather*} p_{t}(d)=P\left(e_{t}(d)=1 \mid \sigma_{t}, x_{t}, r_{t}\right) \end{gather*}$$实现公平就是要消除差异,即各组单位相关度的曝光尽可能一致:
$$\begin{gather*} D_{\tau}^{E}\left(G_{i}, G_{j}\right)=\frac{\frac{1}{\tau} \sum_{t=1}^{\tau} \operatorname{Exp}_{t}\left(G_{i}\right)}{\operatorname{Merit}\left(G_{i}\right)}-\frac{\frac{1}{\tau} \sum_{t=1}^{\tau} \operatorname{Exp}_{t}\left(G_{j}\right)}{\operatorname{Merit}\left(G_{j}\right)} \end{gather*}$$影响力公平的实现方式类似:
$$\begin{gather*} \begin{array}{c} \operatorname{Imp}_{t}\left(G_{i}\right)=\frac{1}{\left|G_{i}\right|} \sum_{d \in G_{i}} c_{t}(d) \\ D_{\tau}^{E}\left(G_{i}, G_{j}\right)=\frac{\frac{1}{\tau} \sum_{t=1}^{\tau} \operatorname{Imp}_{t}\left(G_{i}\right)}{\operatorname{Merit}\left(G_{i}\right)}-\frac{\frac{1}{\tau} \sum_{t=1}^{\tau} \operatorname{Imp}_{t}\left(G_{j}\right)}{\operatorname{Merit}\left(G_{j}\right)} \end{array} \end{gather*}$$无偏性
再回顾一下无偏性的定义:用于描述用户偏好的统计量是无偏的。这里我们需要考虑无偏性的三个变量:
- 位置偏差$p_t$
- 用户与物料的相关性$R(d|x)$
- 全局物料相关性$R(d)$
$R(d|x)$表示物料与用户的真实相关度,例如点击概率,而通常是无法直接观测到实际相关度$r_t$的,只能观测到$c_t$,即用户的点击情况。因此可以使用抽样和因果推断的方法。
抽样指通过多次尝试,借助$c_t$的数学期望来估计$r_t$。
关于因果推断,事件/变量之间的关系,最主要的有相关性和因果性。
- 相关性是指在观测到的数据分布中,X与Y相关,如果我们观测到X的分布,就可以推断出Y的分布
- 因果性是指在操作/改变X后,Y随着这种操作/改变也变化,则说明X是Y的因
cause在常用的机器学习算法中,关注的是特征之间的相关性,而无法去识别特征之间的因果性,而很多时候在做决策与判断的时候,我们需要的是因果性。举个例子,我们会发现在学校中,近视的同学成绩更好。近视和成绩好之间有强相关性,但显然近视不是成绩好的原因。而我们想要提升学生成绩,自然需要找到因,否则就会通过给学生戴眼镜的方式来提高成绩。上面的例子是很明显地可以区分出相关与因果的,但是也有很多难以区分的,如经常喝葡萄酒的人寿命更长,是因为葡萄酒确实能延长寿命,还是因为能经常喝的人通常更富有,享有更好的医疗条件。
因果推断中估算平均处理效应的经典方法包括“倾向性得分匹配”(Propensity Score Matching)、“倾向性得分加权 “(Propensity Score Weighting)等,本文使用加权的方法。因果推断也是一个比较复杂的研究方向,可参考Yishi Lin的博客进行扩展阅读,链接为:
> 因果推断漫谈
本文估计$R(d|x)$,即$r_t$的思路大致是,通过多次尝试,借助$c_t$的数学期望来求$R(d|x)$,但$c_t$是有偏的。因此我们要使$c_t$无偏,然后求得$R(d|x)$的无偏估计。
假设我们可以观测到真实的相关度标签$\left(\mathbf{r}_{1}, \ldots, \mathbf{r}_{\tau}\right)$,一个简单的方法是基于神经网络构建一个回归模型$\hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)$,损失函数使用最小平方误差函数,其中$w$表示该模型的参数:
$$\begin{gather*} \mathcal{L}^{\mathbf{r}}(w)=\sum_{t=1}^{\tau} \sum_{d}\left(\mathbf{r}_{t}(d)-\hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)\right)^{2} \end{gather*}$$
该函数的目标是使$R(d|x_t)$与$r_t(d)$尽可能接近。但由于$\left(\mathbf{r}_{1}, \ldots, \mathbf{r}_{\tau}\right)$是无法获取的,所以定义一个近似相等的目标函数,使用有偏反馈$\left(\mathbf{c}_{1}, \ldots, \mathbf{c}_{\tau}\right)$。新目标函数使用Inverse Propensity Score (IPS) weighting方法来纠正position bias,IPS方法是因果推断中的经典方法,详细资料可参考上文链接,新的目标函数表示为:
$$\begin{gather*} \mathcal{L}^{\mathbf{c}}(w)=\sum_{t=1}^{\tau} \sum_{d} \hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)^{2}+\frac{\mathbf{c}_{t}(d)}{\mathbf{p}_{t}(d)}\left(\mathbf{c}_{t}(d)-2 \hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)\right) \end{gather*}$$新模型中的回归模型表示为$\hat{R}^{\operatorname{Reg}}\left(d \mid \boldsymbol{x}_{t}\right)$。上述目标函数是无偏的,那就是说它的期望应该等于$\mathcal{L}^{\mathbf{r}}(w)$:
$$\begin{gather*} \begin{aligned} \mathbb{E}_{\mathbf{e}} &\left[\mathcal{L}^{\mathbf{c}}(w)\right] \\ &=\sum_{t=1}^{\tau} \sum_{d} \sum_{\mathbf{e}_{t}(d)}\left[\hat{R}^{\mathbf{w}}\left(d \mid \boldsymbol{x}_{t}\right)^{2}+\frac{\mathbf{c}_{t}(d)}{\mathbf{p}_{t}(d)}\left(\mathbf{c}_{t}(d)-2 \hat{R}^{\mathbf{w}}\left(d \mid \boldsymbol{x}_{t}\right)\right)\right] \mathrm{P}\left(\mathbf{e}_{t}(d) \mid \boldsymbol{\sigma}_{t}, \boldsymbol{x}_{t}\right) \\ &=\sum_{t=1}^{\tau} \sum_{d} \hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)^{2}+\frac{1}{\mathbf{p}_{t}(d)} \mathbf{r}_{t}(d)\left(\mathbf{r}_{t}(d)-2 \hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)\right) \mathbf{p}_{t}(d) \\ &=\sum_{t=1}^{\tau} \sum_{d} \hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)^{2}+\mathbf{r}_{t}(d)^{2}-2 \mathbf{r}_{t}(d) \hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right) \\ &=\sum_{t=1}^{\tau} \sum_{d}\left(\mathbf{r}_{t}(d)-\hat{R}^{\mathrm{w}}\left(d \mid \boldsymbol{x}_{t}\right)\right)^{2} \\ &=\mathcal{L}^{\mathbf{r}}(w) \end{aligned} \end{gather*}$$其中$\mathrm{P}\left(\mathbf{e}_{t}(d) \mid \boldsymbol{\sigma}_{t}, \boldsymbol{x}_{t}\right)$表示边缘曝光概率,在曝光模型中就是$p_t(d)$。
最后是$R(d|x)$的简化版本$R(d)$的估计,其无偏估计为:
$$\begin{gather*} \hat{R}^{\mathrm{IPS}}(d)=\frac{1}{\tau} \sum_{t=1}^{\tau} \frac{\mathbf{c}_{t}(d)}{\mathbf{p}_{t}(d)} \end{gather*}$$只要倾向是从0开始有界的,该估计就是无偏的:
$$\begin{gather*} \begin{aligned} \mathbb{E}_{\mathbf{e}}\left[\hat{R}^{\mathrm{IP}}(d)\right] &=\frac{1}{\tau} \sum_{t=1}^{\tau} \sum_{\mathbf{e}_{t}(d)} \frac{\mathbf{e}_{t}(d) \mathbf{r}_{t}(d)}{\mathbf{p}_{t}(d)} \mathrm{P}\left(\mathbf{e}_{t}(d) \mid \boldsymbol{\sigma}_{t}, \boldsymbol{x}_{t}\right) \\ &=\frac{1}{\tau} \sum_{t=1}^{\tau} \frac{\mathbf{r}_{t}(d)}{\mathbf{p}_{t}(d)} \mathbf{p}_{t}(d) \\ &=\frac{1}{\tau} \sum_{t=1}^{\tau} \mathbf{r}_{t}(d) \\ &=R(d) \end{aligned} \end{gather*}$$公平性的动态控制
基于上述公平性衡量方法以及相关的无偏估计量,该文提出了FairCo算法,其思想来源于Proportional Controller,即比例控制器,其核心是为了在常态信号下控制特定信号而构建的一种模型。关于比例控制器,举例说明:
假设有一个水缸,最终的控制目的是要保证水缸里的水位永远的维持在1米的高度。假设初试时刻,水缸里的水位是0.2米,那么当前时刻的水位和目标水位之间是存在一个误差的error,且error为0.8.这个时候,假设旁边站着一个人,这个人通过往缸里加水的方式来控制水位。如果单纯的用比例控制算法,就是指加入的水量u和误差error是成正比的。即
u=kperror
假设kp取0.5,
那么t=1时(表示第1次加水,也就是第一次对系统施加控制),那么u=0.50.8=0.4,所以这一次加入的水量会使水位在0.2的基础上上升0.4,达到0.6.
接着,t=2时刻(第2次施加控制),当前水位是0.6,所以error是0.4。u=0.5*0.4=0.2,会使水位再次上升0.2,达到0.8.
如此这么循环下去,就是比例控制算法的运行方法。
当然上面的例子是存在一些问题的,例如如果水缸漏水怎么办?这也是PID控制算法要解决的问题,扩展阅读:
本文中的常态是根据用户的偏好对内容进行排序,需要控制的是不能让某个组的物料过多的出现,FairCo算法表示为:
$$\begin{gather*} \text { FairCo: } \quad \boldsymbol{\sigma}_{\tau}=\underset{d \in \mathcal{D}}{\operatorname{argsort}}\left(\hat{R}(d \mid \boldsymbol{x})+\lambda \operatorname{err}_{\tau}(d)\right) \end{gather*}$$可以看到,FairCo算法是基于修改后的相关度得分来对物料进行排序的,该分数是$\hat{R}(d \mid \boldsymbol{x})$加上一个误差项$\operatorname{err}_{\tau}(d)$,误差项乘以一个权重参数$\lambda$作为最后用于排序的分数,其中误差项为:
$$\begin{gather*} \operatorname{err}_{\tau}(d)=(\tau-1) \cdot \max _{G_{i}}\left(\hat{D}_{\tau-1}\left(G_{i}, G\right)\right) \end{gather*}$$误差项表示上一个时刻,即$\mathcal{T}-1$时刻物料d所在组与优势(曝光、影响力…)最大组之间的最大差距。对于优势最大的组,误差项对排序的提升帮助为0,而其他组的排序会得到相应提升。
文中证明了随着时间推移,即当$\mathcal{T}$趋向于无穷大时,各个组的平均差距将趋于0,平均差距定义如下:
$$\begin{gather*} \bar{D}_{\tau}=\frac{2}{m(m-1)} \sum_{i=0}^{m} \sum_{j=i+1}^{m}\left|D_{\tau}\left(G_{i}, G_{j}\right)\right| \end{gather*}$$实验结果
文中使用了一个自己的示例进行模拟,用相关的IPS估计器来评估Fairco算法。首先,从广告中抽取新闻文章作为测试数据集,该数据集用两极化得分标记每个新来源。然后模拟访问这个网站的用户,这样每个用户都有一个相关的两极化得分和一个开放性参数。如下图所示:
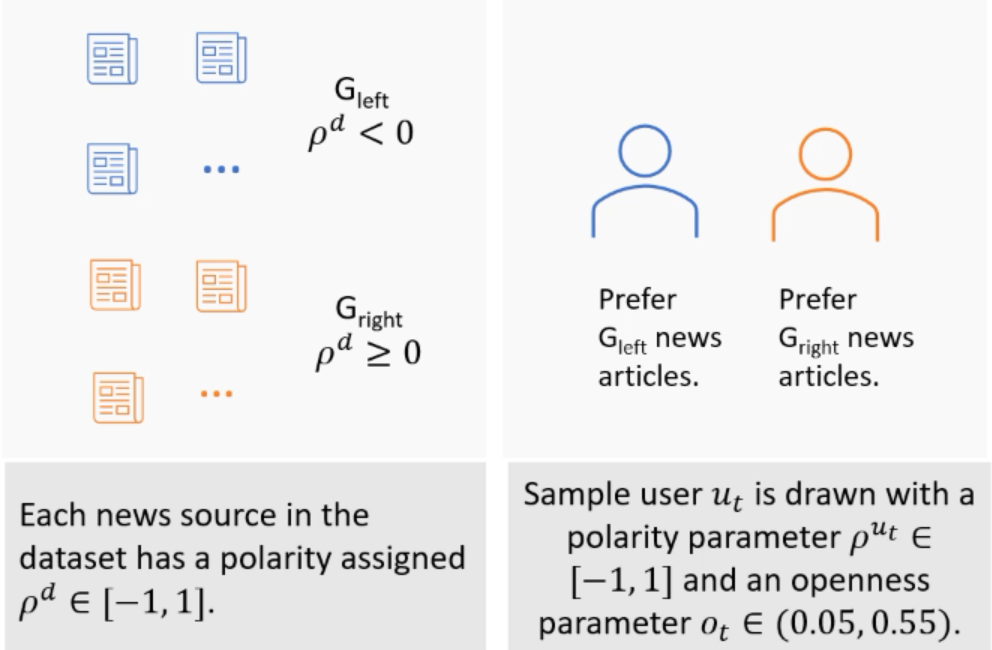
用户与新闻文章的真实相关度是新闻文章的两极化得分和用户开放性参数的函数,其真实相关度分布服从伯努利分布:
$$\begin{gather*} \mathbf{r}_{t}(d) \sim \text { Bernoulli }\left[p=\exp \left(\frac{-\left(\rho^{u_{t}}-\rho^{d}\right)^{2}}{2\left(o^{u_{t}}\right)^{2}}\right)\right] \end{gather*}$$在第一个实验中对一些右偏向性用户进行模拟,右偏向性用户可以通过在G-right文章中引入点击来偏向排名。可以看到公平控制器Fairco能从最初的偏差中恢复过来,同时仍在学习相关度,如下图所示:
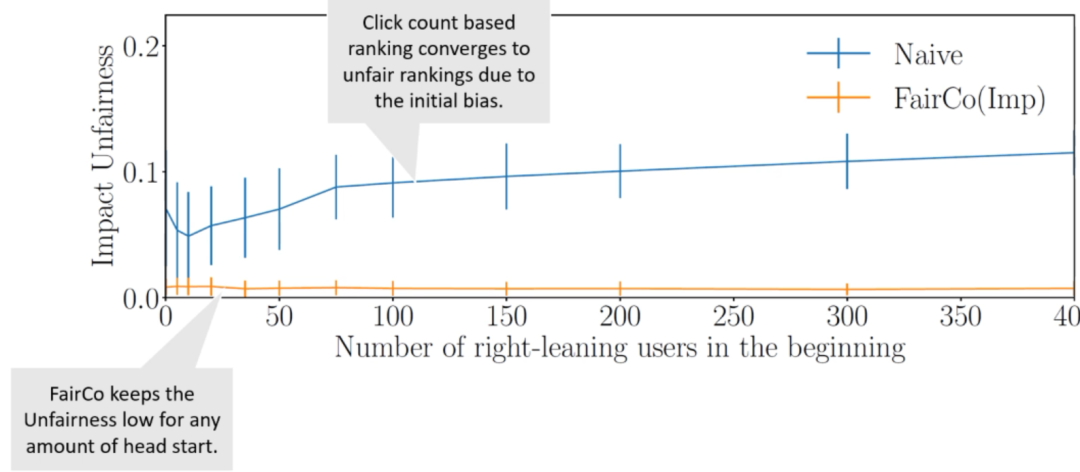
未经调整的排名算法很难打破最初少数用户造成的偏差,即使某些“富人”在一开始就有大量的领先优势,Fairco也能够将这种偏差减少到零,并将不公平性保持在较低水平。这就意味着最开始的“富人”是有破产的风险的,但是某些“富人”也可能会继续受用户“偏爱”而富下去。
如果我们改变左偏向性用户在用户群体中的比例,Fairco可以始终将不公平性保持在接近零的水平,同时在其中一个群体占多数的情况下以公平换取效用,如下图所示:
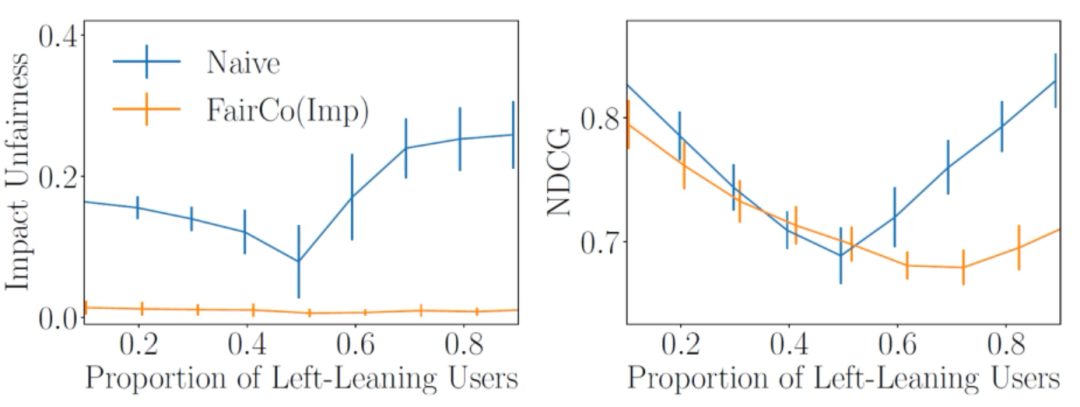
这也对应了文章开头举的一些例子,例如在热搜场景中,FairCo算法可能就不是很适合,因为类似场景是要强化“马太效应”的,而FairCo算法为了公平会牺牲一些效用。相反在商品推荐等场景中我们要关注公平性,这时FairCo算法可得到相应使用。