SimHash和MinHash算法主要应用于海量文本查重,两者都属于局部敏感哈希(Locality-Sensitive Hashing, LSH)算法,而LSH又是近似最近邻查找(Approximate Nearest Neighbor, ANN)中的一类算法,其主要思想是利用降维和索引,加快查找过程。
SimHash
算法的过程如下图所示:
具体过程为:
- 确定文本Doc中各个词语(中文需分词)的权重,方法可以有多种,例如TfIdf和TextRank算法,则文档可表示为(feature, weight)组成的向量;
- 初始化一个长度为64位(可综合空间和时间复杂度考虑具体数值)的Doc特征向量,各元素初始化为0;
- 对Doc中每个词语利用hash函数计算一个长度为64位的特征向量;
- 遍历词语特征向量,如果第i位为1,则Doc特征向量对应位+w,否则-w;
- 所有词语处理完毕后,判断Doc特征向量的每一位,如果大于0,则置1,否则置0;
- 获得各Doc的特征向量后,可利用海明距离判断两篇文档的相似性,一般地,距离<=3时认为两者是相似的。
上述过程可以理解为Doc的特征降维过程,我们将降维后的特征向量称为fingerprints。完成降维后,我们需要思考如何设计索引来加快查找过程。
第一种方案是对查询向量Q进行变化,查找64位所有3位以内的变化的组合,如下图所示:
单一内容Q需要进行四万多次查询,时间复杂度太高。
第二种方案是对已生成Doc的fingerprints进行3位以内的组合变化,但需要多占据四万多倍的原始空间,如下图所示:
如何找到一种空间和时间的平衡呢?假设海明距离在3以内的两个文档是相似的,那么只要将64位的二进制串分为4块,根据鸽巢原理,两个文档的fingerprints中至少有一块是完全相同的,如下图所示:
由于查询时无法预知是哪一块区域相同,因此需要对四块中的每一块都建立索引,假设样本库中有$2^{32}$个,约43亿的fingerprints,那么每个table中包含$2^{32-16}$=65536个候选结果,大大减少了海明距离的计算成本。上图所示的索引结构在MongoDB中实现非常简单。此外,索引块数k和table中候选结果数量m也是一个平衡抉择的过程,k越大,m越小,空间复杂度升高;k越小,m越大,时间复杂度升高。下图是k=4时索引示意图:
MinHash
与SimHash不同,MinHash要从衡量两个文档的相似度说起。Jaccard相似度用于描述两个集合的相似程度,假设有两个集合A和B,相似度=A与B交集的元素个数/A与B并集的元素个数,公式为:
$$\begin{gather*}
J(A, B)=\frac{|A \cap B|}{|A \cup B|}
\end{gather*}$$
海量文本直接求Jaccard相似度复杂度太高,两个文档需要逐个词比较,为降低复杂度,我们使用两个文档的最小哈希值相等的概率来等价于两个文档的Jaccard相似度,并可以证明两者是相等的。首先说明一下如何求一个集合的最小哈希值,假设现在有4个集合,分别为S1,S2,S3,S4;其中,S1={a,d}, S2={c}, S3={b,d,e}, S4={a,c,d},所以全集U={a,b,c,d,e}。我们可以构造如下0-1矩阵:
| 元素 | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| a | 1 | 0 | 0 | 1 |
| b | 0 | 0 | 1 | 0 |
| c | 0 | 1 | 0 | 1 |
| d | 1 | 0 | 1 | 1 |
| e | 0 | 0 | 1 | 0 |
为得到各集合的最小哈希值,首先对矩阵进行随机行打乱,则某个集合(某一列)的最小哈希值就等于打乱后第一个值为1的行所在的行号。定义一个最小哈希函数h,用于模拟对矩阵进行随机打乱,假设打乱后的矩阵如下表所示:
| 元素 | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| b | 0 | 0 | 1 | 0 |
| e | 0 | 0 | 1 | 0 |
| a | 1 | 0 | 0 | 1 |
| d | 1 | 0 | 1 | 1 |
| c | 0 | 1 | 0 | 1 |
则h(S1)=2, h(S2)=4, h(S3)=0, h(S4)=2。经过随机打乱后,两个集合的最小哈希值相等的概率=两集合的Jaccard的相似度证明如下:
仅考虑集合S1和S2,那么这两列所在的行有以下三种情况:
- S1和S2的值都为1,用X表示;
- 一个值为1,另一个为0,用Y表示;
- S1和S2的值都为0,用Z表示。
S1与S2的交集元素个数为X,并集个数为X+Y,所以sim(S1,S2)=Jaccard(S1,S2)=X/(X+Y)。随机打乱后h(S1)=h(S2)的概率等于从上往下扫描,在遇到Y行之前遇到X行的概率(Z行没有影响),或者说把X个黑球和Y个白球放入一个袋子中,首次拿到黑球的概率,即h(S1)=h(S2)的概率为X/(X+Y)。假设特征矩阵很大时,对其进行打乱非常耗时,而且要进行多次打乱,其实可以通过多个随机哈希函数来模拟打乱的效果。具体地,定义n个随机哈希函数$h_1, h_2,…,h_n$,sig(i,j)表示签名矩阵中第i个哈希函数在第j列上的元素,将签名矩阵中各个元素sig(i,j)初始化为inf(无穷大),对原矩阵中每一行r:
- 计算$h_1(r),h_2(r),...,h_n(r)$;
- 对于每一列j:
- 如果j所在的第r行为0,什么都不做;
- 如果j所在的第r行为1,则对每个i=1,2,…,n,$sig(i,j)=min(sig(i,j), h_i(r))$
例如$h_1(x)=(x+1)%5, h_2(x)=(3*x+1)%5$,则经过上述操作可获得如下的签名矩阵:
| 哈希函数 | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| $h_1$ | 1 | 3 | 0 | 1 |
| $h_2$ | 0 | 2 | 0 | 0 |
上述获得各文档签名矩阵可以理解为一个降维过程,获得签名后,假如数据量十分庞大的话,两两比较的话计算复杂度仍然非常高,所以需要类似SimHash索引分块的方法来降低查询复杂度。当一个新文档到达时,希望仅比较与其相似性较高的文档,忽略相似性较低的集合。如下图所示,假设签名矩阵有12行,我们将3行为一组放进一个“桶”里: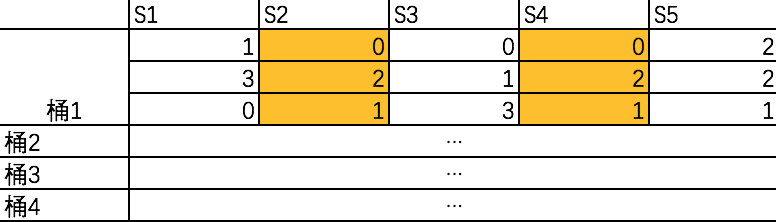
对于S2,仅需要查询与其具有相同桶的集合,如下图所示: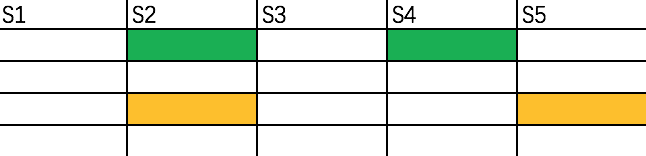
即只需要查询S4和S5。
参考资料
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.295.8001&rep=rep1&type=pdf
https://blog.csdn.net/heiyeshuwu/article/details/44117473
https://www.cnblogs.com/sddai/p/6110704.html