搜索和推荐系统一般包含召回和排序两个阶段，搜索排序主要关注相关性，常见的模型可以参考搜索排序算法。推荐模型则关注用户偏好，一般用CTR点击率来描述，常用的推荐模型有：

图片来源：推荐算法炼丹笔记：CTR点击率预估系列入门手册

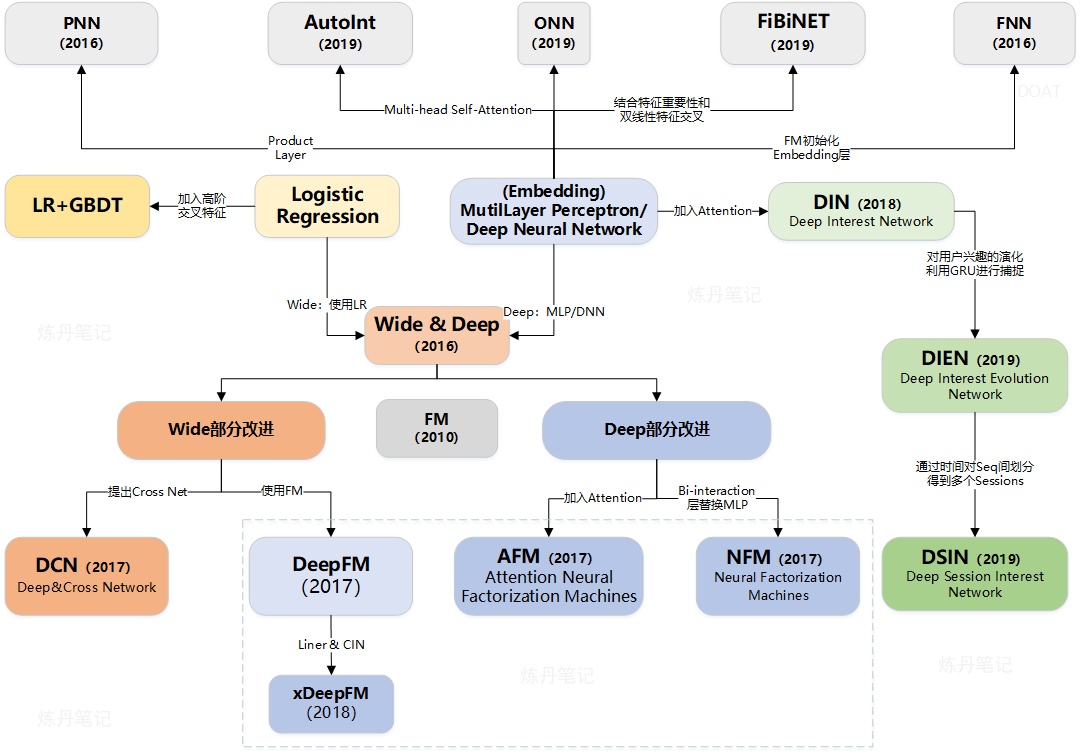
本文重点关注应用较为广泛的LR、GBDT、FM、Wide&Deep和DIN模型，其中LR、GBDT和FM部分大部分图片引用自刘启林的机器学习笔记。

模型介绍

LR

下面从逻辑回归LR的假设、原理和训练等方面进行介绍。

LR假设

数据服从伯努利分布；
样本概率是Sigmoid函数。

LR原理

逻辑回归模型是由线性回归模型和Sigmoid函数共同组成的：

Sigmoid函数：

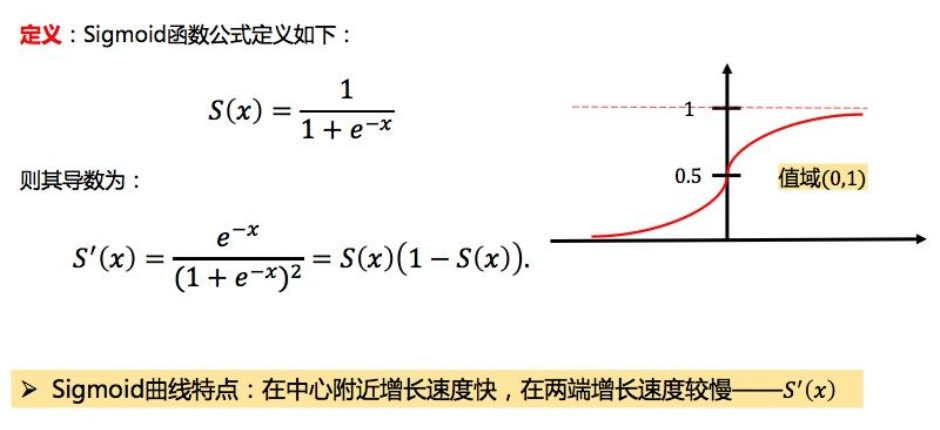
线性回归定义：

线性回归假设：

一元线性回归：

多元线性回归：

线性回归模型：

回到逻辑回归，LR一般用于分类任务，其中二分类的原理如下：

LR训练

根据二项分布构建似然函数，为方便进行训练转化为对数似然函数，并通过极大似然估计方法进行参数训练：

极大似然估计是一种参数估计方法，使用的前提条件是：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量，且有充分的训练样本。极大似然估计（Maximum Likelihood Estimation）的原理可以用下图说明：

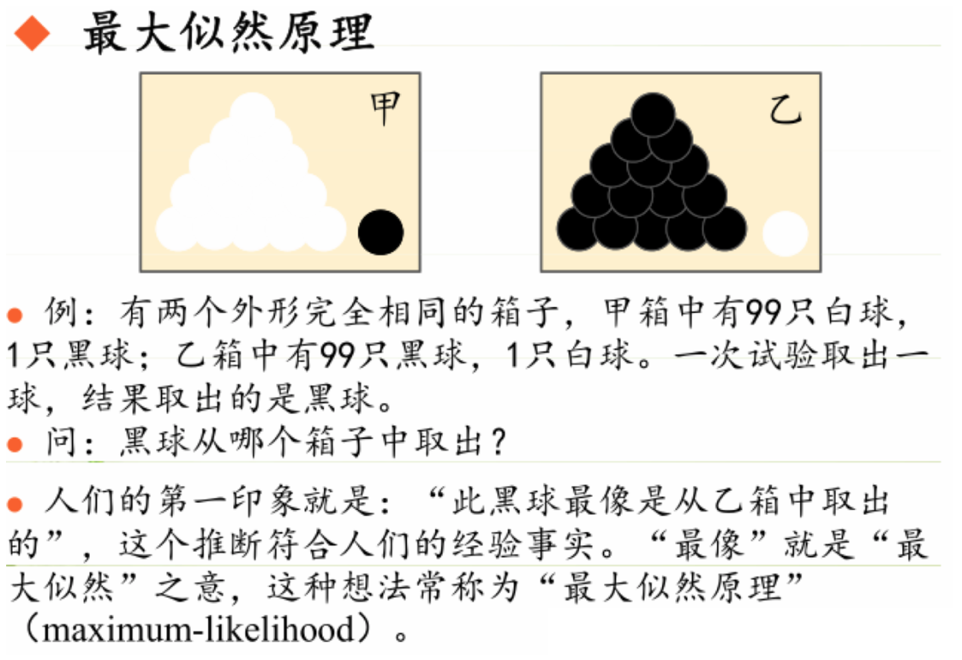
极大似然估计的目的：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值，即：“模型已定，参数未知”。

考虑一个样本集$D=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$，我们需要对参数$\theta$进行估计。似然函数定义为联合密度函数$p(D \mid \theta)$：

$l(\theta)=p(D \mid \theta)=p\left(x_{1}, x_{2}, \ldots, x_{n} \mid \theta\right)=\prod_{i=1}^{n} p\left(x_{i} \mid \theta\right)$

如果$\hat{\theta}$是参数空间中使似然函数最大的$\theta$值，那么$\hat{\theta}$应该就是“最可能”的参数值，$\hat{\theta}$就是$\theta$的极大似然估计量。联合密度函数连乘求导比较麻烦，一般取对数后转换为叠加进行求解。

利用梯度下降法进行训练：

LR梯度下降公式还是很简洁的：

而在训练模型时，我们通常使用损失函数，这里如果取整个数据集上的平均对数似然损失可以得到：$J(w)=-\frac{1}{N} \ln L(w)$

显然在逻辑回归模型中，最大化似然函数和最小化损失函数其实是等价的。

LR扩展知识点

优缺点

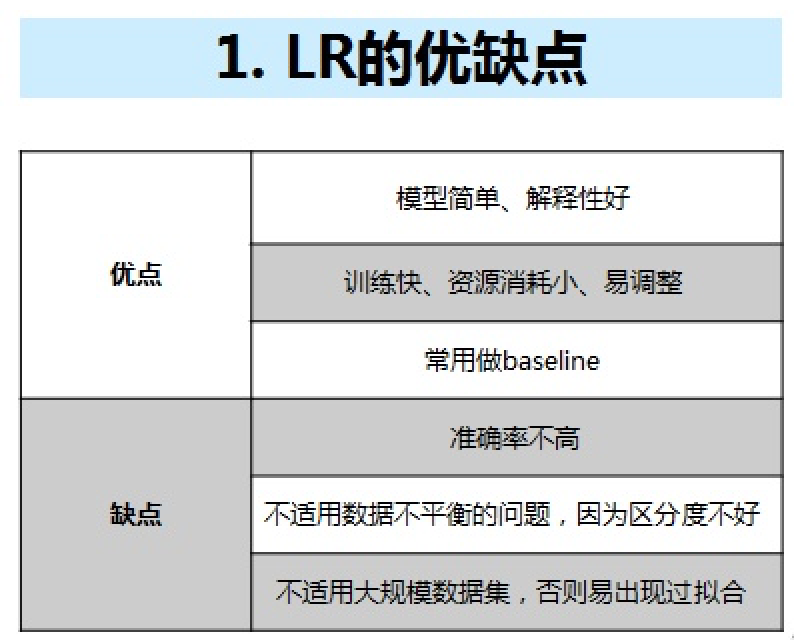
对比线性回归

多分类

多项逻辑回归

Softmax回归：

损失函数

为什么不使用平方误差作为损失函数？

平方误差损失函数加上sigmoid的函数将会是一个非凸的函数，不易求解，会得到局部解，用对数似然函数得到高阶连续可导凸函数，可以得到最优解。
对数损失函数更新起来很快，因为只和x，y有关，和sigmoid本身的梯度无关。如果使用平方损失函数，会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。

特征离散化

为什么逻辑回归一般会进行特征离散化处理：

非线性：逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；离散特征的增加和减少都很容易，易于模型的快速迭代；
速度快：稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
鲁棒性：离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
方便交叉与特征组合：离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
稳定性：特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；
简化模型：特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。

正则化

用于避免过拟合，一般采用L1或L2正则化。L1 正则的本质其实是为模型增加了“模型参数服从零均值拉普拉斯分布”这一先验知识，L1会趋向于产生少量的特征，而其他的特征都是0(稀疏性)。 L2 正则的本质其实是为模型增加了“模型参数服从零均值正态分布”这一先验知识，L2会选择更多的特征，这些特征都会接近于0。L1在特征选择时候非常有用，而L2只是一种规则化。L1范数可以使权值稀疏，方便特征提取。L2范数可以防止过拟合，提升模型的泛化能力。

FM

FM（Factor Machine，因子分解机）是一种基于矩阵分解的机器学习算法，用于解决大规模稀疏矩阵中特征组合问题，可以看做针对上文中提到的线性模型的改进，回顾一下线性回归模型：

线性回归模型假设特征之间是相互独立的、不相关的。但在现实的某些场景中，特征之间往往是相关的，而不是相互独立的。比如<女人>和<化妆品>，<男人>与<足球>等，所以需要特征组合。一种简单的做法是将特征进行两两组合，如下图所示：

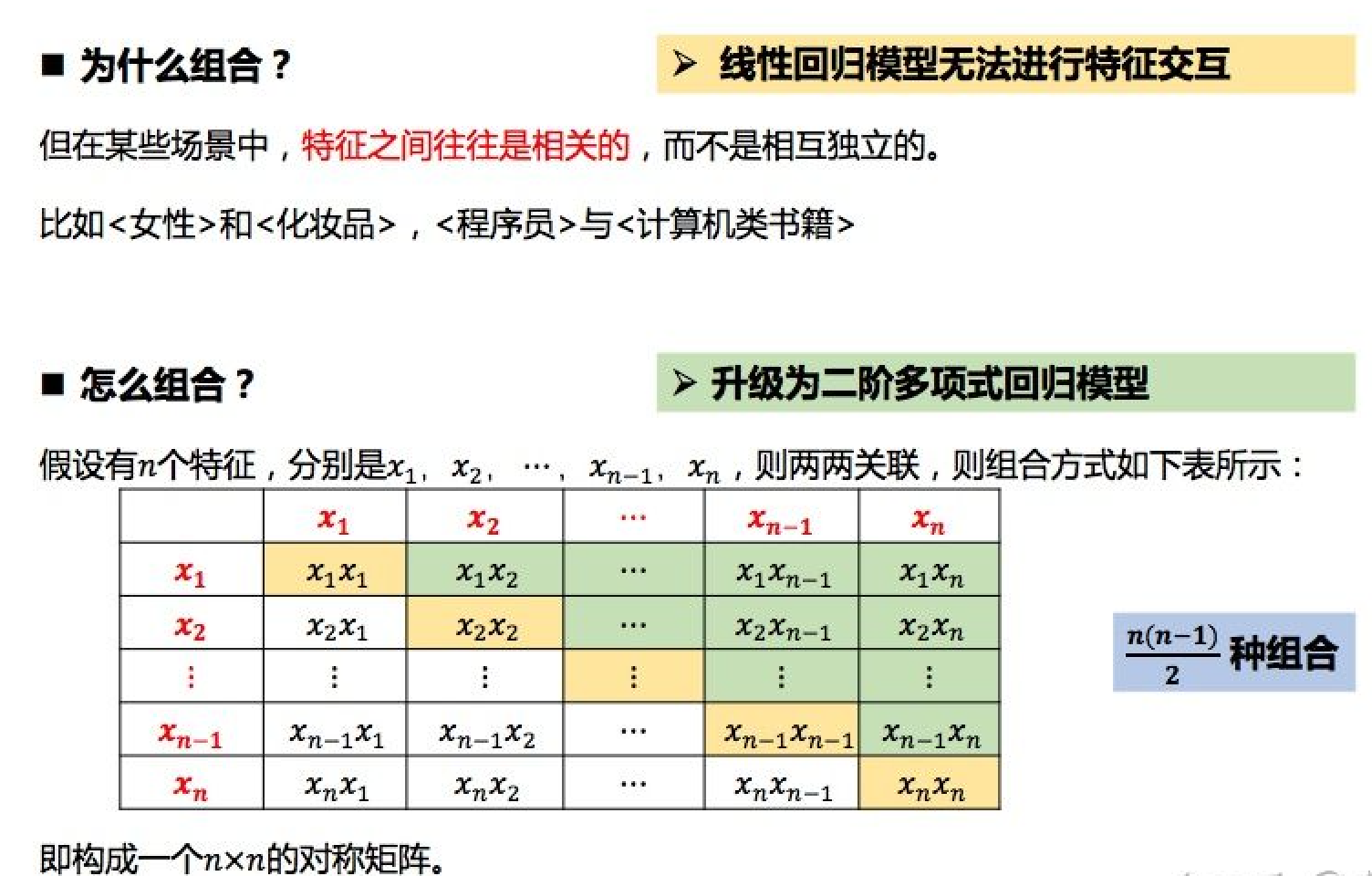
我们可以利用二阶多项式回归模型对此进行建模：

矩阵分解(Matrix Factorization) vs 因子分解机(Factor Machine)

MF（Matrix Factorization，矩阵分解）在推荐系统已经得到广泛应用，最典型的代表就是协同过滤模型。其核心思想是通过两个低维小矩阵（一个代表用户embedding矩阵，一个代表物品embedding矩阵）的乘积计算，来模拟真实用户点击或评分产生的大的协同信息稀疏矩阵，本质上是编码了用户和物品协同信息的降维模型，如下图所示：

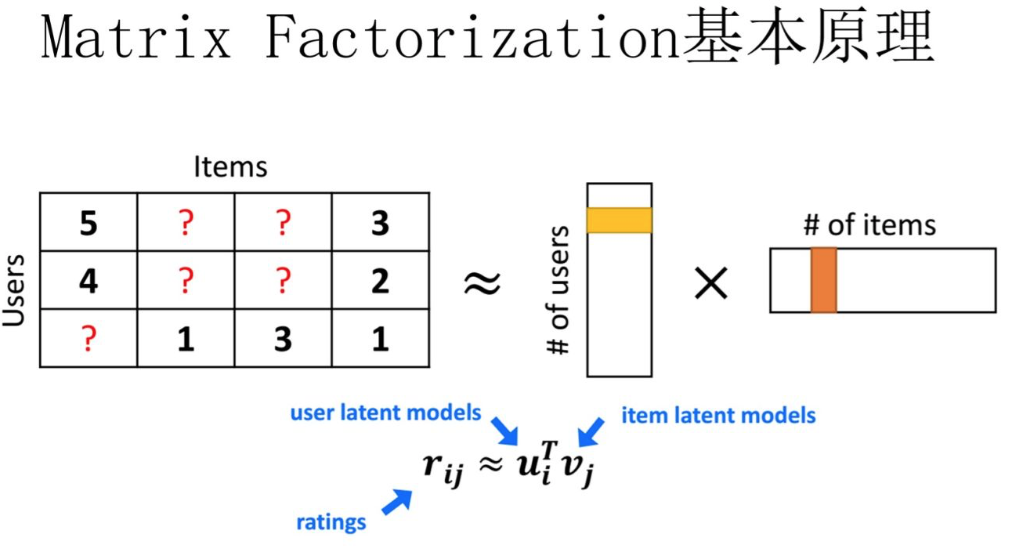
图片来源：推荐系统召回四模型之：全能的FM模型

当训练完成，每个用户和物品得到对应的低维embedding表达后，如果要预测某个$User_{i}$对$Item_{j}$ 的评分的时候，只要它们做个内积计算$<User_{i},Item_{j}>$ ，这个得分就是预测得分:

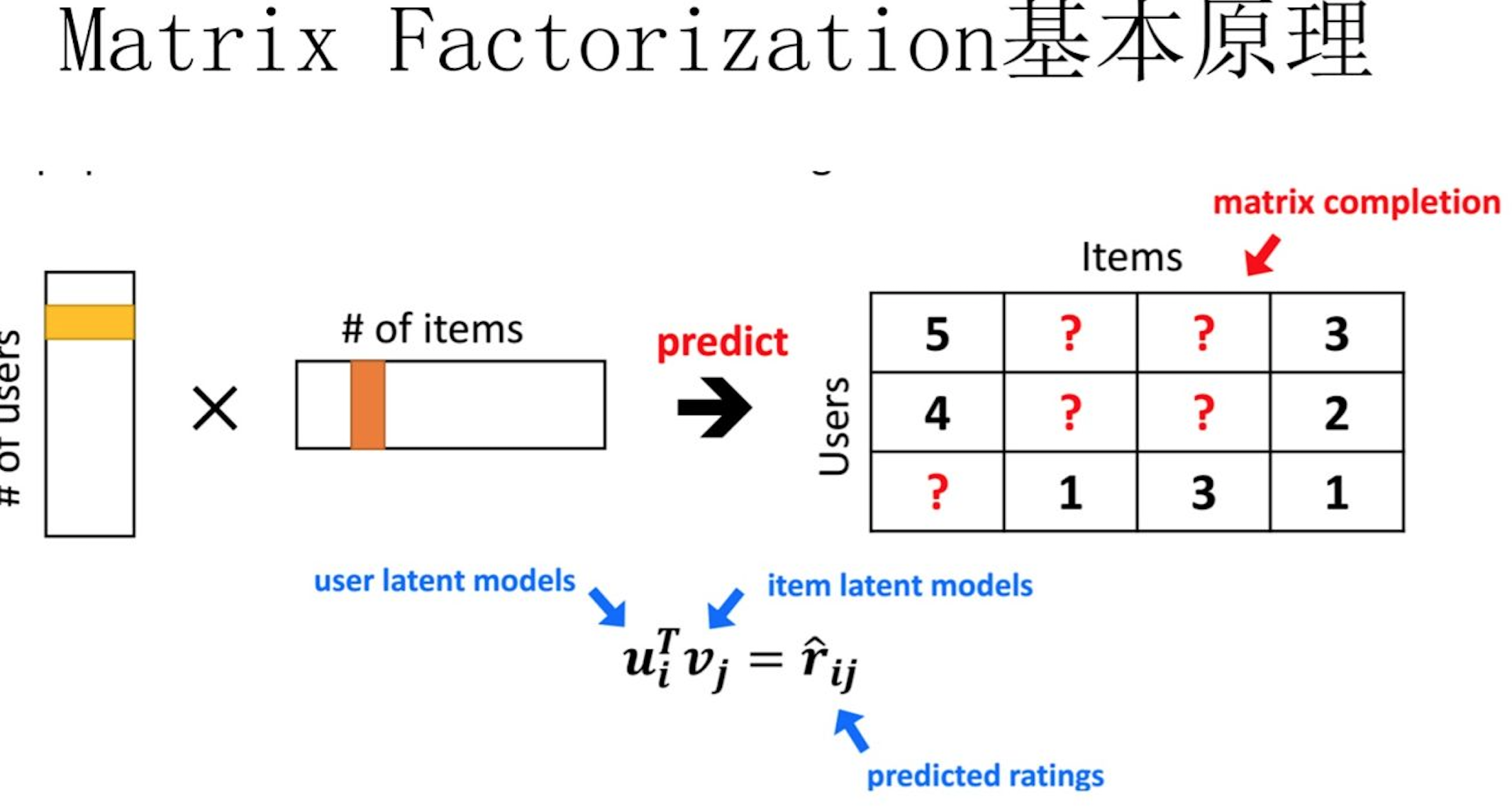
MF和FM不仅在名字简称上看着有点像，其实他们本质思想上也有很多相同点。本质上，MF模型是FM模型的特例，MF可以被认为是只有User ID 和Item ID这两个特征Fields的FM模型，MF将这两类特征通过矩阵分解，来达到将这两类特征embedding化表达的目的。而FM则可以看作是MF模型的进一步拓展，除了User ID和Item ID这两类特征外，很多其它类型的特征，都可以进一步融入FM模型里，它将所有这些特征转化为embedding低维向量表达，并计算任意两个特征embedding的内积，就是特征组合的权重，如下图所示：

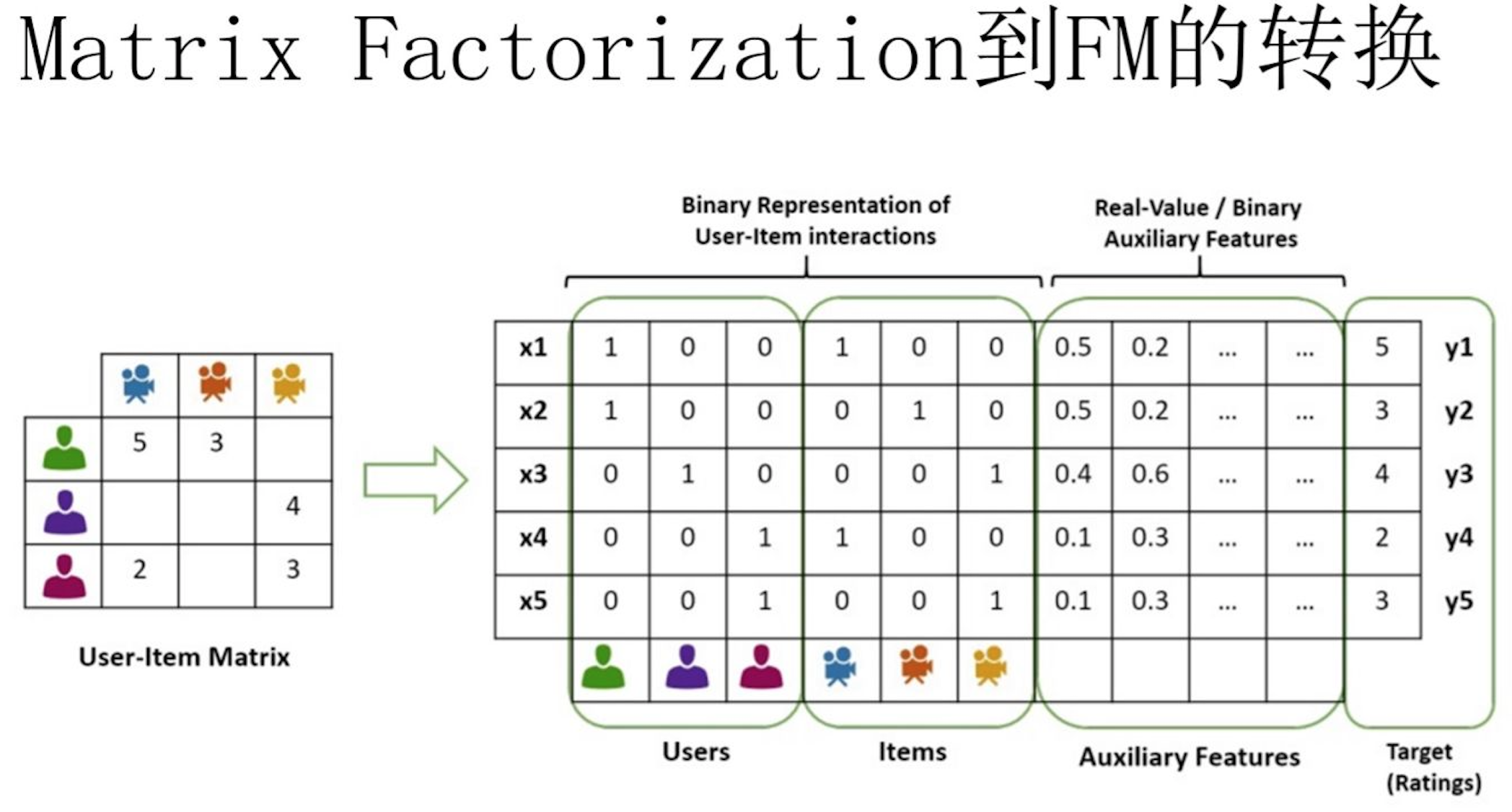
FM模型原理

从下图中公式可以看出，公式前半部分是线性模型，后半部分是特征交叉项。因此多项式回归模型的特征组合能力要强于线性模型，而当交叉项参数全部为0时退化为普通的线性模型。由于实际场景中，数据往往非常稀疏，因此对于二次项参数的训练是很困难的。因为对于每个参数$w_{i,j}$需要大量的$x_{i}$和$x_{j}$均不为0的样本进行训练，但由于往往样本比较稀疏，这很容易导致参数$w_{i,j}$不准确，最终将严重影响模型的性能。解决这一问题的方法是给每个特征分量$x_{i}$引入一个辅助向量$v_{i}=(v_{1},v_{2},...,v_{k})$，然后利用$v{i}*v{j}$对参数$w_{i,j}$进行估计，如下图所示：

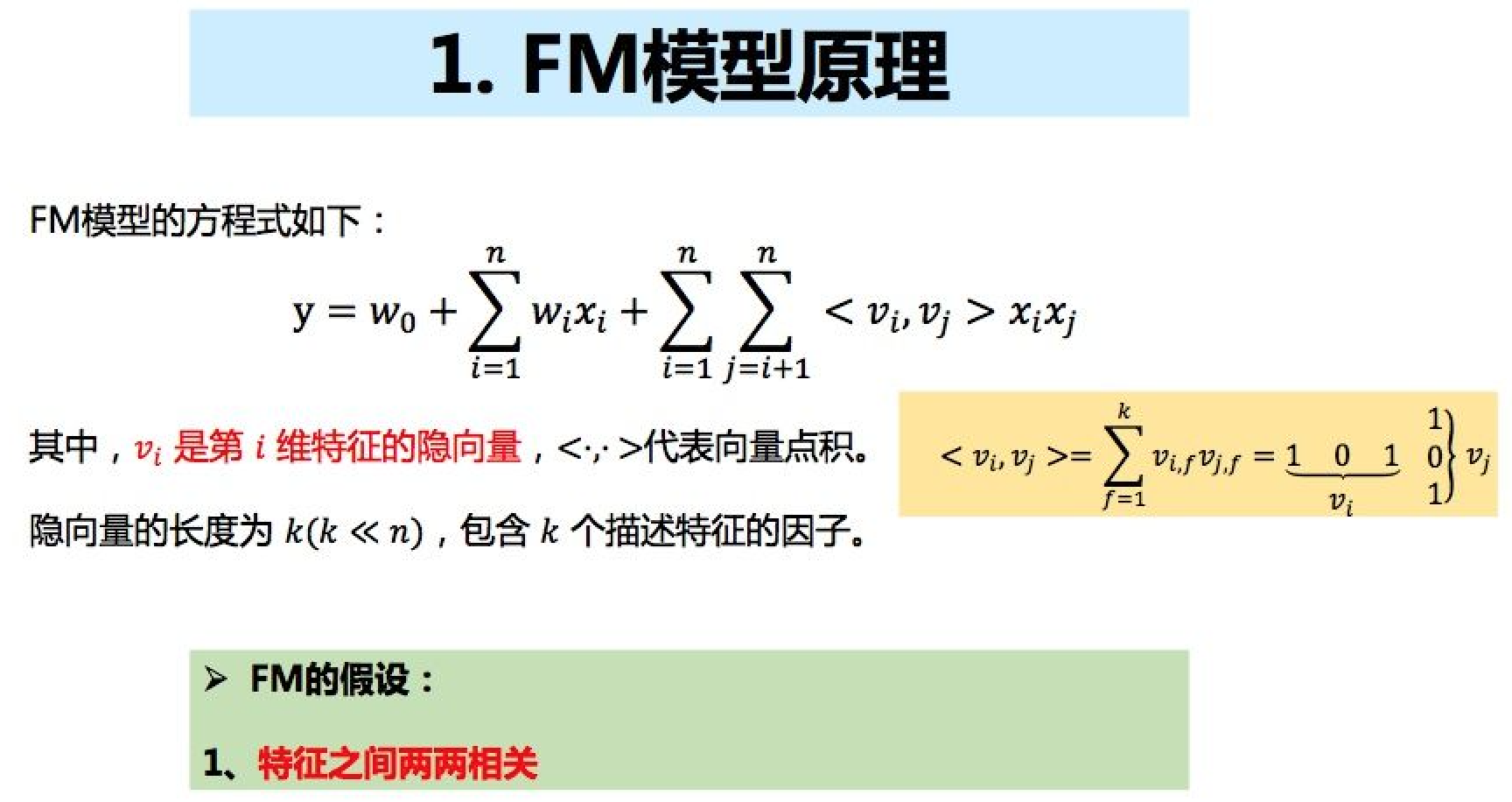
FM模型训练

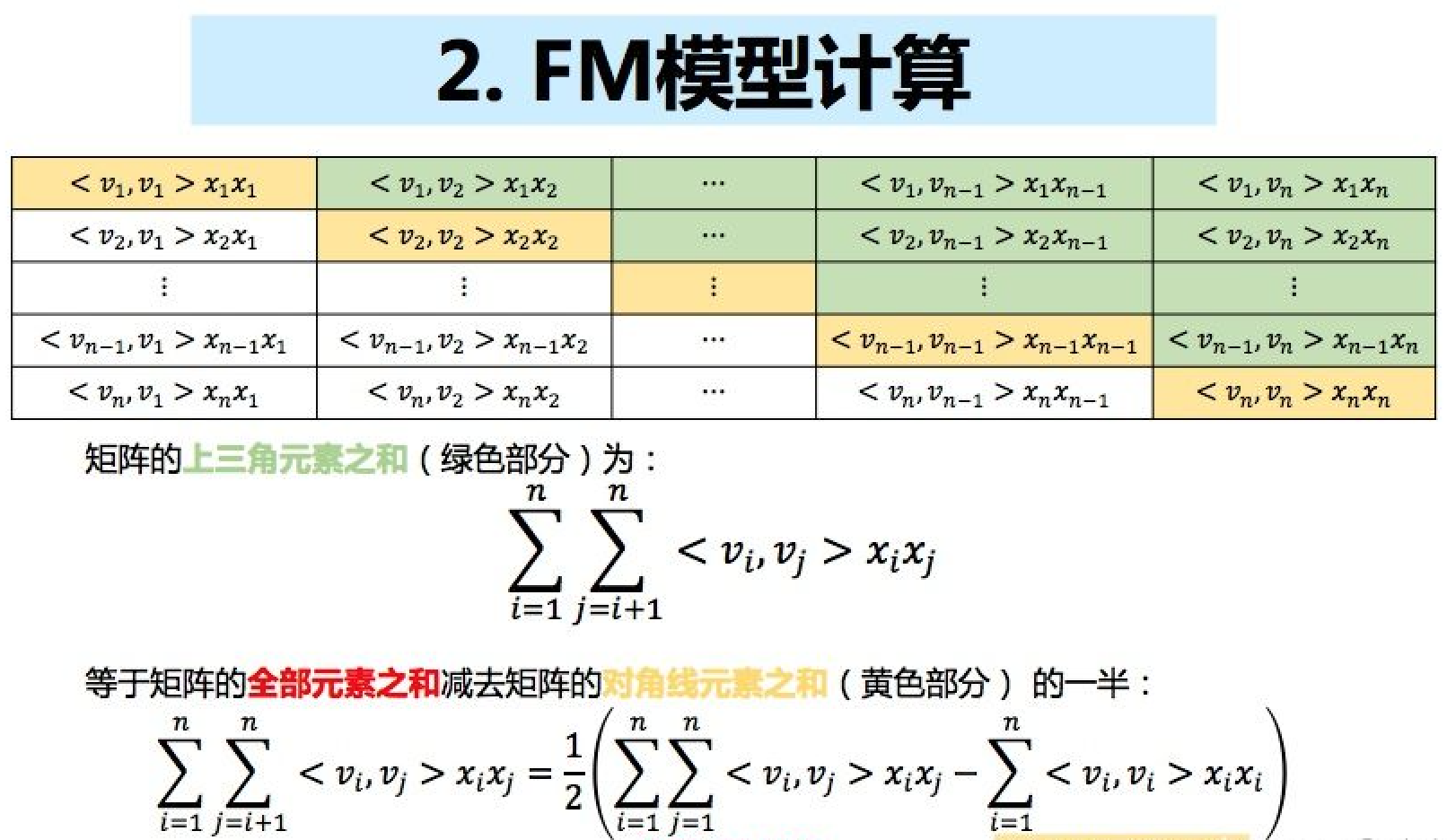
对于FM原始模型可以看到参数的复杂度是$O(n^2)$的，那么如何降低这一复杂度呢？可以通过下面的过程进行化简：

化简后的参数复杂度为$O(n)$，降低至线性复杂度：

FM模型训练：

采用随机梯度下降：

FM模型特征工程：

FM模型应用

FM模型可应用于回归、分类和排名任务中，参考原论文中的应用方式：

回归任务可使用平方误差损失函数：

$$\begin{gather*} \text {Loss}=\frac{1}{2} \sum_{i=1}^{n}\left(\hat{y}_{i}-y_{i}\right)^{2} \end{gather*}$$

求偏导，得到：

$$\begin{gather*} \frac{\partial L}{\partial \hat{y}(x)}=(\hat{y}(x)-y) \end{gather*}$$

则梯度为：

$$\begin{gather*} \frac{\partial L}{\partial \theta}=(\hat{y}(x)-y) * \frac{\partial \hat{y}(x)}{\partial \theta} \end{gather*}$$

分类任务可使用对数损失函数：

$$\begin{gather*} \text { Loss }=\frac{1}{2} \sum_{i=1}^{n}-\ln \left(\sigma\left(\hat{y}_{i} y_{i}\right)\right)^{2} \end{gather*}$$

其中：

$$\begin{gather*} \sigma(\hat{y} y)=\frac{1}{1+e^{-\hat{y} y}} \frac{\partial(\sigma(\hat{y} y))}{\partial \hat{y}}=\sigma(\hat{y} y) *[1-\sigma(\hat{y} y)] * y \end{gather*}$$

对数损失函数的梯度为：

$$\begin{gather*} \begin{array}{c} \frac{\partial L}{\partial \theta}=\frac{1}{\sigma(\hat{y} y)} * \sigma(\hat{y} y) *\left[1-\sigma(\hat{y} y] * y * \frac{\partial \hat{y}(x)}{\partial \theta}\right. \\ =[1-\sigma(\hat{y} y)] * y * \frac{\partial \hat{y}(x)}{\partial \theta} \end{array} \end{gather*}$$

排序任务可先利用FM模型获得分数，然后利用pairwise分类损失函数进行训练，当然也有多种求解方式，可参考搜索排序算法。

FM模型扩展知识点

FM模型优点：

适用于数据稀疏场景。

线性回归 vs FM：

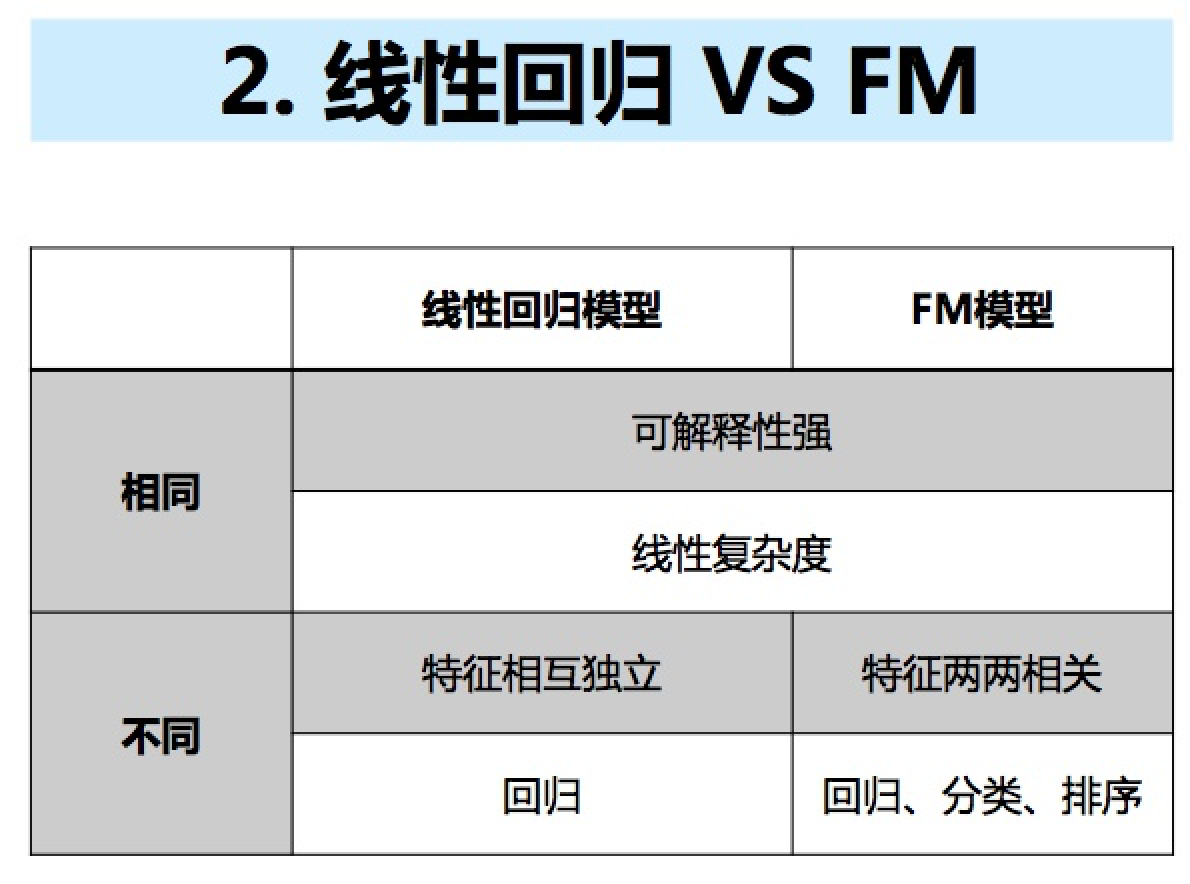
FM模型演化：

FFM(Field Factorization Machine)是在FM的基础上引入了“场（Field）”的概念而形成的新模型。在FM中计算特征$x_i$ 与其他特征的交叉影响时，使用的都是同一个隐向量 $V_i$ 。而FFM将特征按照事先的规则分为多个场(Field)，特征 $x_i$属于某个特定的场f。每个特征将被映射为多个隐向量 $V_{i 1}, \ldots, V_{i f}$ ，每个隐向量对应一个场。当两个特征$x_i,x_j$ ,组合时，用对方对应的场对应的隐向量做内积:$w_{i j}=\mathbf{v}_{i, f_{j}}^{T} \mathbf{v}_{j, f_{i}}$

FFM 由于引入了场，使得每两组特征交叉的隐向量都是独立的，可以取得更好的组合效果， FM 可以看做只有一个场的 FFM。

DeepFM模型将深度神经网络模型与FM模型结合，模型结构如下图所示：

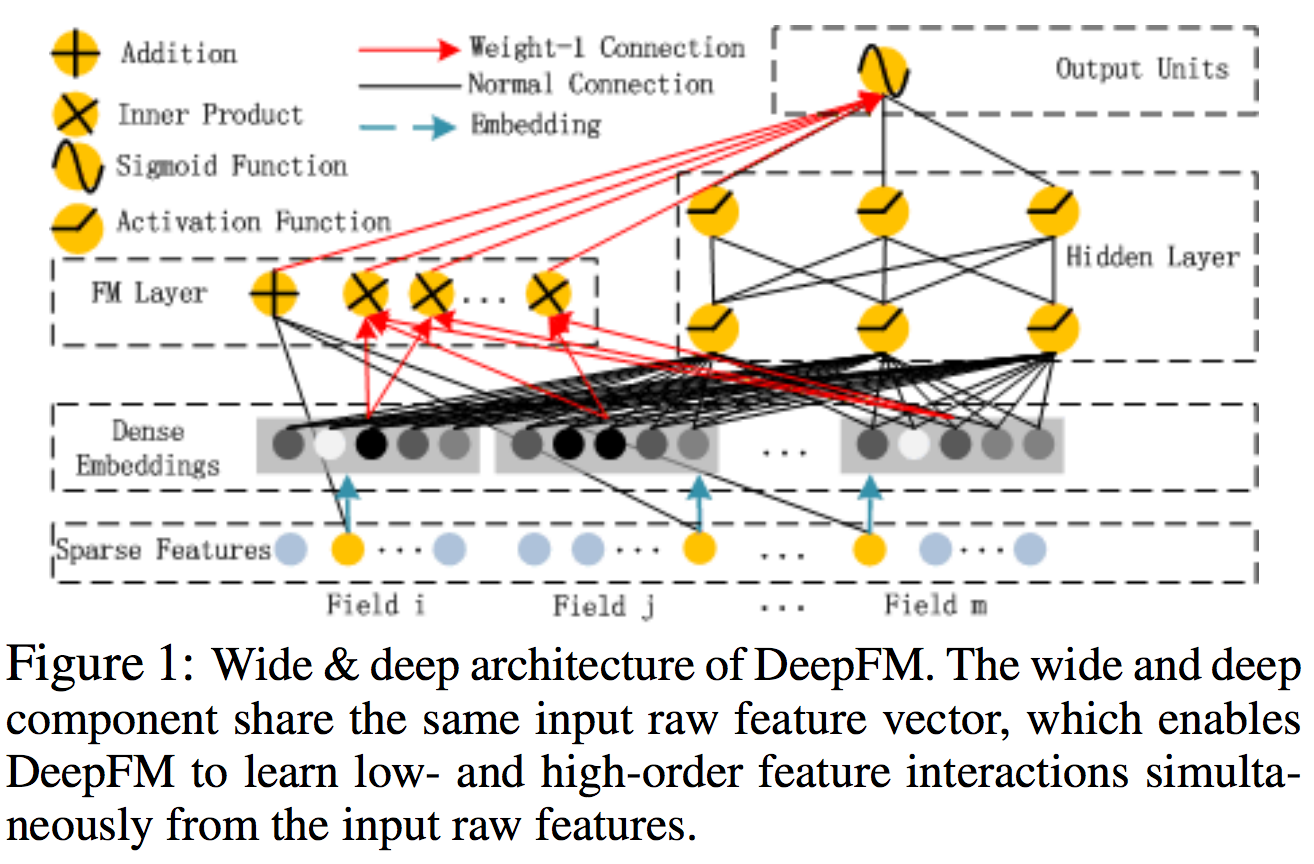
模型分为两部分：FM（左边）和DNN（右边）：

首先利用FM进行embedding得到Dense Embeddings的输出;
将Dense Embeddings的结果作为左边FM模型和右边DNN模型的输入。通过一定方式组合后，模型左边FM模块的输出完全模拟出了FM的效果，而右边的DNN模块则学到了比FM模块更高阶的交叉特征。
最后将DNN和FM的结果组合后输出。

GBDT

关于GBDT已在LambdaMART从放弃到入门一文中进行了介绍，具体可参考其中MART部分对于BT和GBT的介绍，本文只提取一些要点。理解GBDT要从决策树DT开始，然后是BT，再到GBT。梯度提升树BT用于分类模型时，是梯度提升决策树GBDT；用于回归模型时，是梯度提升回归树GBRT，二者的区别主要是损失函数不同。李航老师在《统计学习方法》一书中对决策树的基础和原理进行了详细介绍，网上也有不少笔记资料，例如李航统计学习方法-决策树。这里做一下简单总结：

决策树通常包含三个步骤：特征选择、自顶向下生成和自底向上剪枝；
决策树通常分为三种，如下图所示：

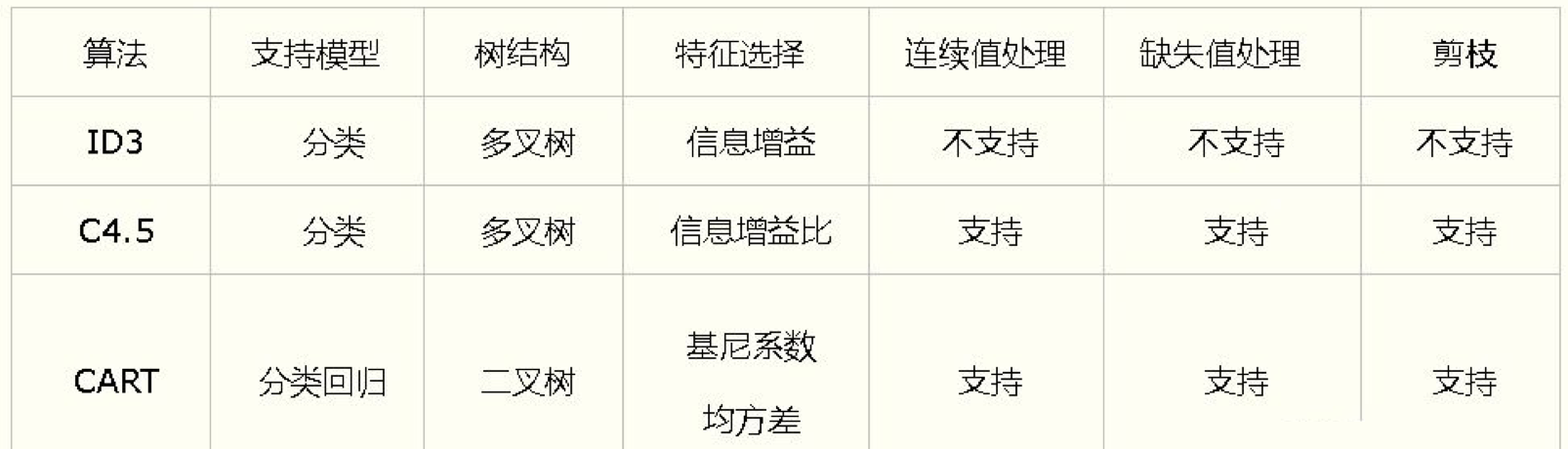
图片来自：《统计学习方法》（第五章）决策树

BT(Boosting Tree)提升树是以决策树为基本学习器的提升方法，它被认为是统计学习中性能最好的方法之一。提升树模型可以表示为决策树为基学习器的加法模型，其学习思想有点类似一打高尔夫球，先粗略的打一杆，然后在之前的基础上逐步靠近球洞，也就是说每一棵树学习的是之前所有树预测值和的残差，这个残差就是一个加预测值后得到真实值的累加量。不同问题的提升树学习算法主要区别在于使用的损失函数不同，（设预测值为$\tilde{y}$ ，真实值为$\hat{y}$):

回归问题：通常使用平方误差损失函数$L(\tilde{y}, \hat{y})=(\tilde{y}-\hat{y})^{2}$。
分类问题：通常使用指数损失函数：$L(\tilde{y}, \hat{y})=e^{-\tilde{y} \hat{y}}$

而当损失函数不是平方损失函数或指数损失函数时，由于求导复杂，导致每一步优化非常麻烦。针对这个问题，Freidman提出了梯度提升树算法(GBT)，其核心思想是利用损失函数的负梯度在当前模型的值作为残差的近似值，本质上是对损失函数进行一阶泰勒展开，从而拟合一个回归树。

XGBoost是对GBDT的进一步优化，主要改进点在于对损失函数进行二阶泰勒展开、加入正则化项和并行化处理等方面。

XGBoost优缺点：

XGBoost vs GBDT:

XGBoost相关论文：

Wide&Deep

W&D模型由谷歌在DLRS 2016会议上提出，其核心思想是结合线性模型的记忆能力和深度模型的泛化能力，从而提升整体性能。记忆能力是指模型直接从历史数据中发现相关性，学习规则的能力，泛化能力指相关性的传递，即模型可以发现在历史数据中很少或者没有出现的特征组合、相关性。以点外卖为例，记忆能力可以推荐我们点过的外卖，或者与点过外卖强相关的外卖（类似商家、同样菜系），而泛化能力可以增加口味的多样性，例如每次都推煲仔饭也总有吃够的时候，泛化能力可以提供一些其他选择，例如烤鱼什么的。

模型原理

谷歌提出的Wide&Deep模型中Wide部分使用广义线性模型LR，Deep部分使用深度神经网络DNN，值得注意的是Wide&Deep不仅仅可以当做一个模型，而是可以作为一个推荐模型的框架，如本文开头的常见推荐模型图所示，我们可以对Wide和Deep部分进行改进。

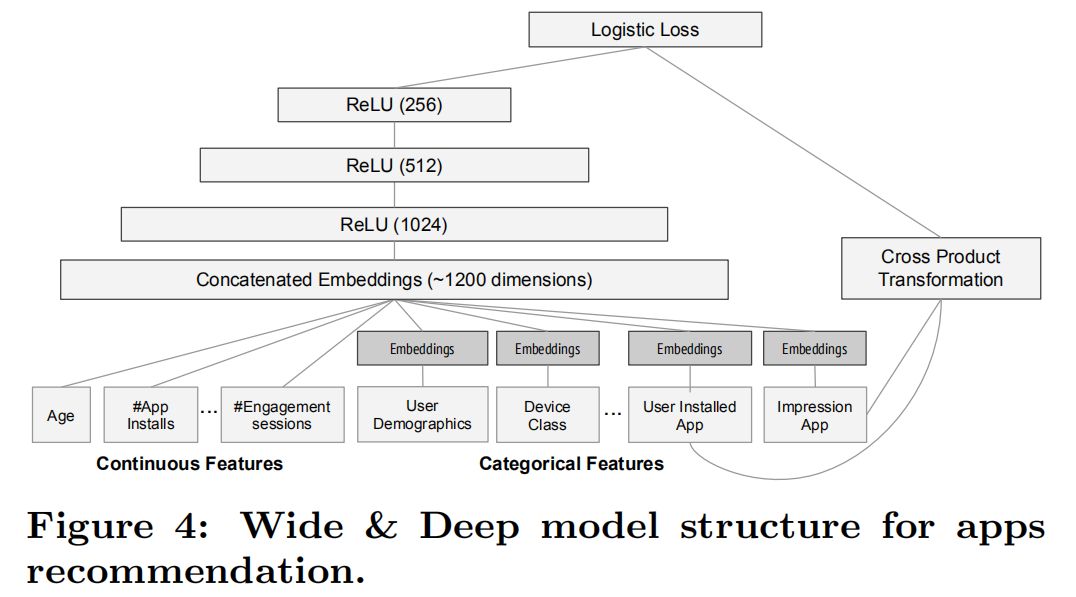
谷歌提出的W&D模型如下图所示：

Wide部分使用广义线性模型：$y=\boldsymbol{w}^{T}[\boldsymbol{x}, \phi(\boldsymbol{x})]+b$

其中x表示原始特征，$\phi(\boldsymbol{x})$ 表示交叉特征。交叉特征定义为：$\phi_{k}(\mathbf{x})=\prod_{i=1}^{d} x_{i}^{c_{k i}} \quad c_{k i} \in\{0,1\}$

$c_{k i}$ 是一个布尔变量，当第i个特征是第k个变化的一部分时取1。对于二值特征，组合后的特征当且仅当原特征都为1时取1，这为广义线性模型增加了非线性能力。

Deep部分使用前馈神经网络：$\boldsymbol{a}^{l+1}=f\left(\boldsymbol{W}^{l} \boldsymbol{a}^{l}+\boldsymbol{b}^{l}\right)$

其中$\boldsymbol{a}^{l}, \boldsymbol{b}^{l}, \boldsymbol{W}^{l}$分别表示第l层的激活值、偏置和权重，f是激活函数。

模型最终输出为：

$$\begin{gather*} P(Y=1 \mid \mathbf{x})=\sigma\left(\mathbf{w}_{\text {wide }}^{T}[\mathbf{x}, \phi(\mathbf{x})]+\mathbf{w}_{\text {deep }}^{T} a^{\left(l_{f}\right)}+b\right) \end{gather*}$$

其中Y表示分类标签，$\sigma(.)$是sigmoid函数，$\phi(x)$是原始特征x的跨产品变换，b是偏置项， $w_wide$是wide模型的权重向量， $w_deep$是用于最终激活函数 $a^(lf)$的权重。

损失函数选取logistic loss，也就是经常使用的交叉熵损失函数。

模型特征

谷歌将模型应用于Google Play商店的APP推荐，使用了年龄、已下载APP和设备类型等特征。注意Wide部分选择了记忆用户已安装的APP与被曝光APP之前的相关性，旨在推荐一些强相关的APP，可以理解为用户装了某个APP后还会装什么，例如安装了淘宝后推荐天猫、拼多多。

模型训练

Wide部分使用带L1正则化的FTRL（Followed the Regularized Leader）算法进行训练，FTRL扩展阅读

在线优化求解

FTRL是一种在线学习算法，可简单理解为一个稀疏性较好、精度不错的随机梯度下降算法，由于是随机梯度下降，因此可以在获取新的样本后进行训练，从而实现模型在线更新。那么Wide部分为何要注重正则化呢？上面模型特征部分已经提到，Wide部分使用的交叉特征是用户已安装APP和当前曝光APP，当两个ID类特征进行组合时，会产生维度爆炸的问题，并且会让原本已经十分稀疏的特征更加稀疏，所以需要利用正则化对海量特征进行过滤方便线上部署。

Deep部分使用常用的AdaGrad算法进行训练，由于输入已经是Age、#App Installs这些数值类特征，或者稠密化的Embedding向量，因此Deep部分不会存在很严重的特征稀疏问题。

DIN

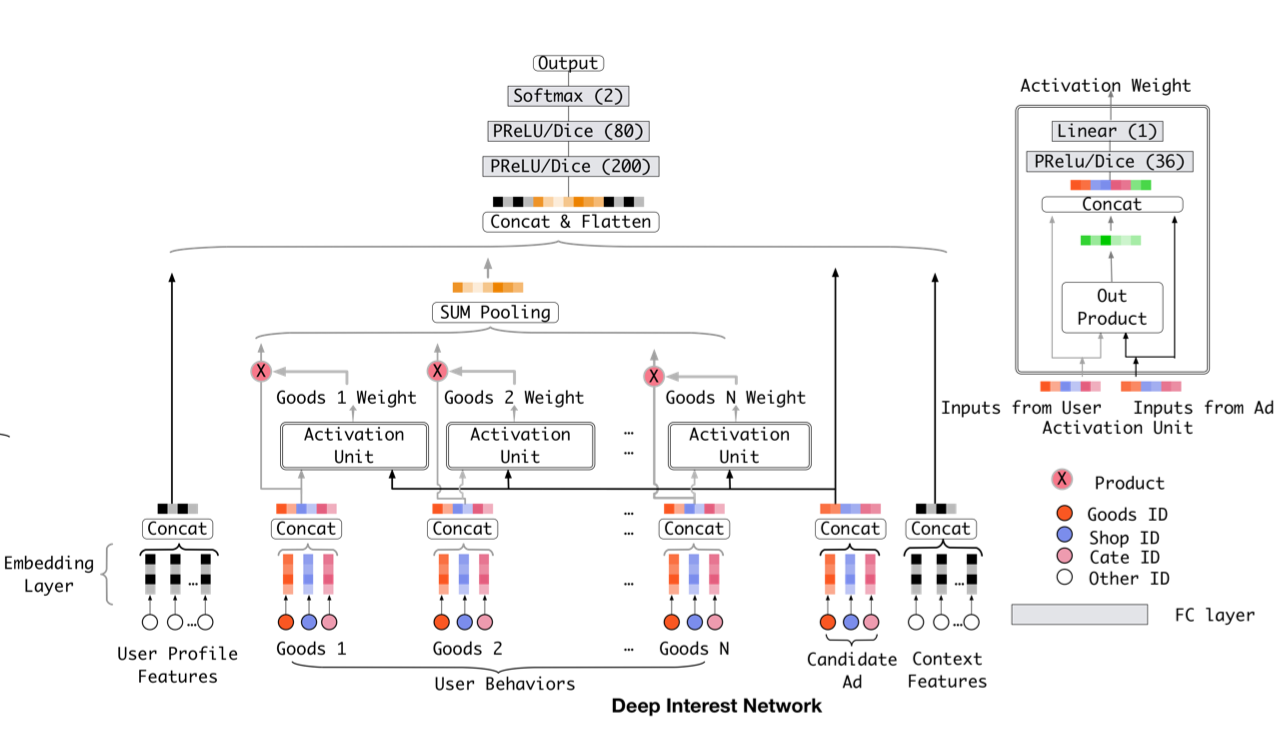
DIN模型在KDD 2018会议上提出，其核心是利用一个局部激活单元来更好的表征用户信息，增强用户信息与候选广告的相关性，这与在CV和NLP领域得到广泛应用的Attention思想其实是一致的。就Wide&Deep框架来看，DIN模型是对于Deep部分的改进，我们先看一下Base Model：

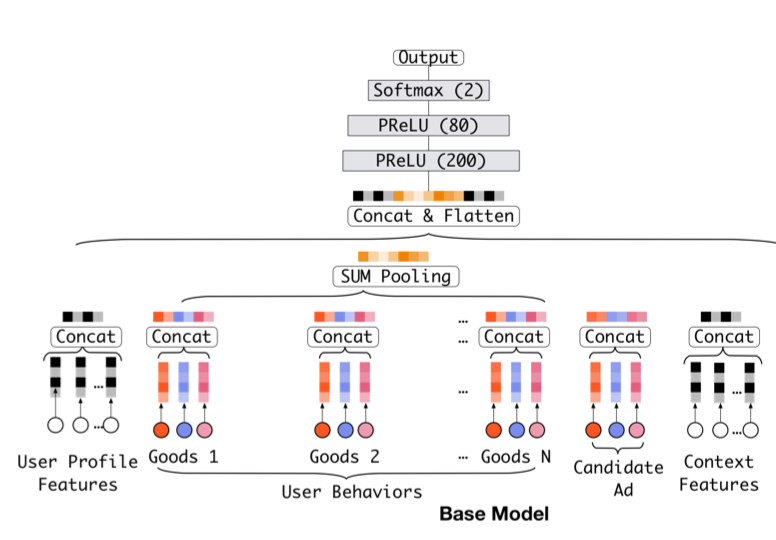
Base Model

Base Model采用深度模型常见的Embedding+MLP方案，首先将大规模稀疏特征映射为Embedding向量，然后利用sum pooling转换为固定长度的向量，最后进行拼接输入到MLP学习特征与预测结果之间的关系，损失函数采用交叉熵损失函数。该模型的缺陷在于无法表达用户兴趣的多样性，因为对于不同的候选广告，模型都将用户的信息表征为一个固定向量，但对于某个候选广告，用户历史行为对于是否点击该广告的影响力一般是不一样的。例如用户历史行为中包含购买电脑、外套和篮球等信息，对于当前的鼠标广告，显然历史行为中的电脑购买信息影响力更大。显然我们可以利用Attention机制对用户侧信息进行更准确的表征，利用候选广告与用户行为的关系计算权重，辅助特征与结果的相关性学习，最终提高模型性能。

DIN Model

DIN模型引入了一个设计的局部激活单元，作用是计算候选广告与用户各行为的权重，在给定候选广告A的基础上自适应地的计算用户信息的表示：

$$\boldsymbol{v}_{U}(A)=f\left(\boldsymbol{v}_{A}, \boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \ldots, \boldsymbol{e}_{H}\right)=\sum_{j=1}^{H} a\left(\boldsymbol{e}_{j}, \boldsymbol{v}_{A}\right) \boldsymbol{e}_{j}=\sum_{j=1}^{H} \boldsymbol{w}_{j} \boldsymbol{e}_{j}$$

其中$\left\{e_{1}, e 2, \ldots e H\right\}$ 表示用户向量，$v_{A}$ 表示候选广告向量，$a(\cdot)$表示前向传播网络。不同于Attention机制的是，$\sum_{i} w_{i}=1$ 的约束被放宽，因此输出权重的softmax归一化也不再采用，目的是表征更强烈的用户兴趣。

对于用户行为的序列特征，不免不产生一个想法，使用RNN、LSTM等建模会有助于提升效果吗？作者也利用LSTM模型进行了尝试，但是由于用户历史行为序列可能包含了多个并发的兴趣，不同兴趣点的快速跳跃和突然终结也会使用户行为的序列特征显得杂乱无章，但是一个可研究的方向。

训练技巧

Mini-batch Aware Regularization。正则化可以防止模型过拟合，但对于工业数据集来说，直接应用传统的正则化方法是不实际的，因为具有大规模稀疏输入和海量的参数。作者提出了一种有效的小批量处理感知型正则化器，它仅针对每个微型批处理中出现的稀疏特征的参数计算L2-范数。
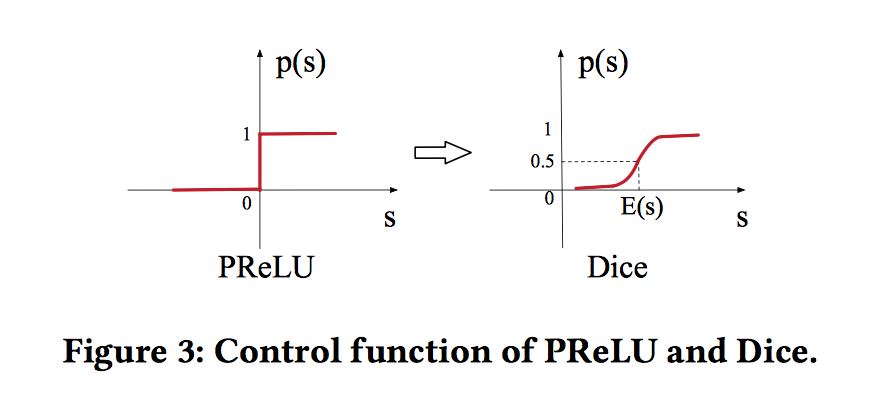
Data Adaptive Activation Function。PRelu是常用的激活函数，采用值为0的硬修正点：
$$f(s)=\left\{\begin{array}{ll} s & \text { if } s>0 \\ \alpha s & \text { if } s \leq 0 \end{array}=p(s) \cdot s+(1-p(s)) \cdot \alpha s\right.$$
当每层的输入遵循不同分布时，这可能不适合。作者设计了一个新的激活函数Dice：
$$\begin{gather*} f(s)=p(s) \cdot s+(1-p(s)) \cdot \alpha s, p(s)=\frac{1}{1+e^{-\frac{s-E[s]}{\sqrt{\operatorname{var}[s]+\epsilon}}}} \end{gather*}$$
其中E[s]和Var[s]分别表示均值和方差，$\epsilon$是一个常量，值为$10^-8$ 。Dice的关键思想是根据输入数据的分布来自适应地调整修正点，其值设置为输入的平均值。当$E[s]=0,Var[s]=0$则退化为PRelu。

两个函数图像如下图所示：

总结

回顾一下文章开头展示的常用推荐模型，我们以Wide&Deep模型为中心进行梳理，本文介绍的LR、FM和GBDT属于Wide部分，而DIN则属于Deep部分。

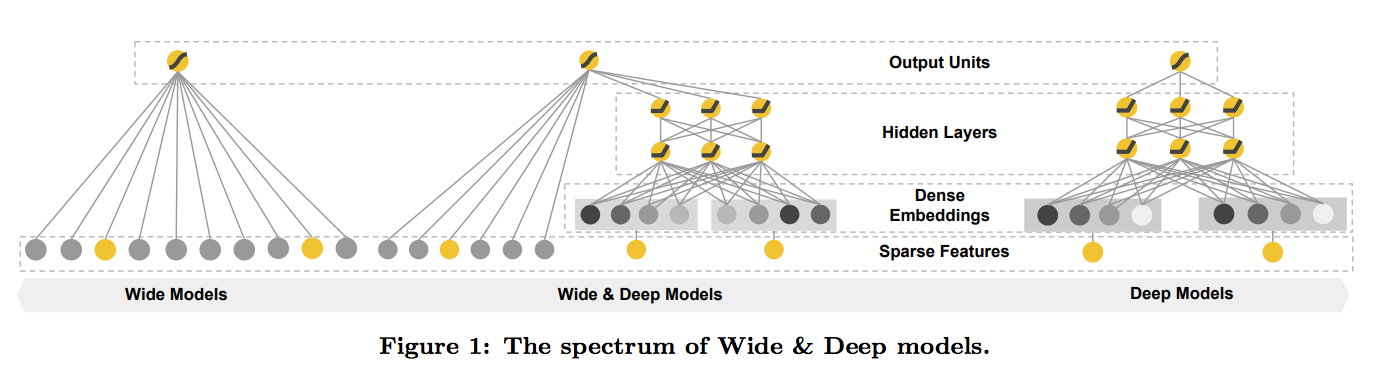
那么从Wide模型到Deep模型的迭代过程大致是什么样的，各个模型有何优缺点呢？这里引用搜索排序算法一文的图片：

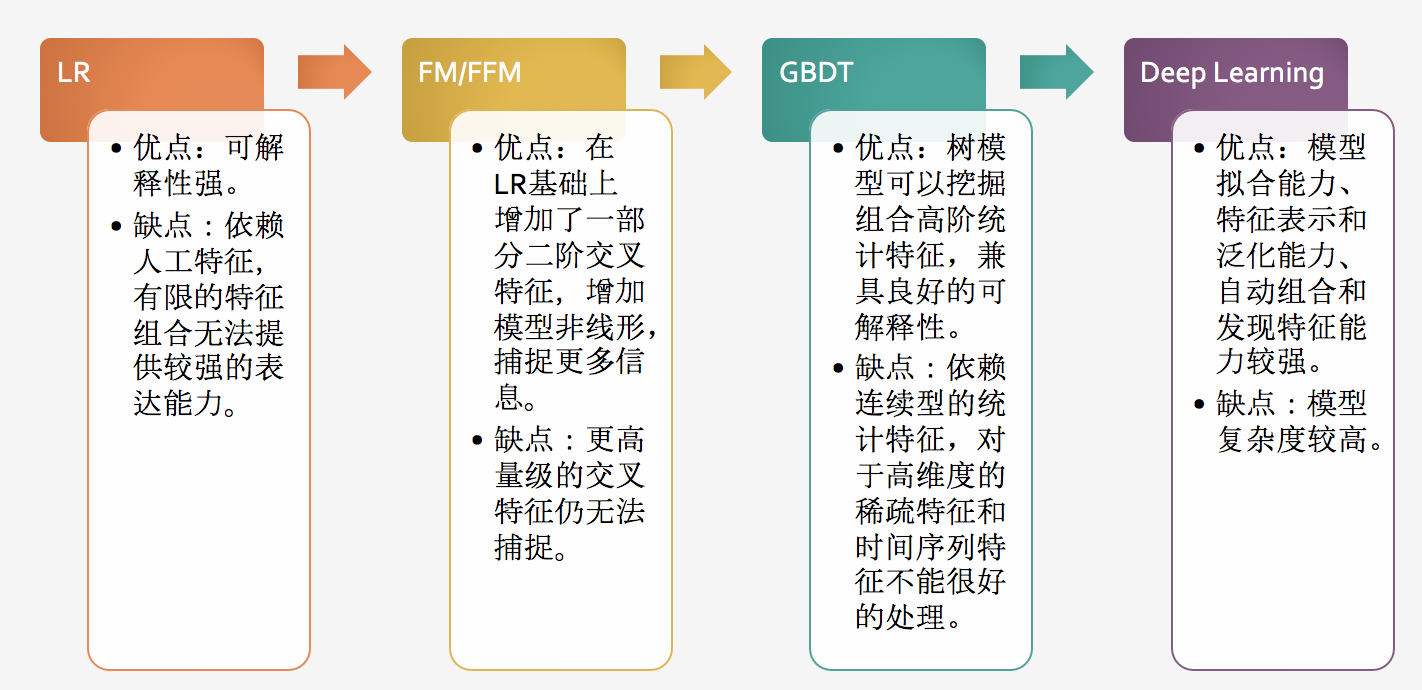
从迭代过程看，模型特征表征能力逐渐增强，复杂度逐渐变高。值得注意的是由于深度模型十分复杂，可解释性很差，所以Wide模型在特定场景下是有用武之地的。例如谷歌论文里Wide部分用于APP的初始推荐，搜索排序系统中的时效模型，Wide模型适用于明确规则、便于人工干预的场景。近些年来的研究主要集中在Deep部分，开始应用Attention机制、GRU等在CV和NLP领域常用的技术。但在工业界，LR、GBDT目前还是在广泛使用，因为深度模型的训练和上线部署都比较复杂，如果效果没有得到显著提升，使用深度模型的性价比不高。所以需要针对特定场景和数据进行仔细分析，选择合适的模型。