业界广泛流传着这样的一句话:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限。特征体系的设计、优化是取得理想结果的基础,那么对于文本搜索,应该如何设计特征呢?本文讨论常见的文本搜索场景,输入为query,目标是将相关性较高的文章排在前面。关于模型,可参考搜索排序算法。
特征分类
特征可以大致分为以下几类:
- 覆盖特征。用于衡量doc对query词语的覆盖程度。
- 命中特征。用于衡量query词语在doc中的匹配情况,代表是BM25算法。
- 紧密特征。用于衡量query词语在doc命中的分布情况。
- 权重特征。用于衡量doc对query需求的满足程度,例如当query为某个学校时(复旦大学), 查询“招生”和“考研”的需求一般会高于“运动会”和“晚会”。
- 语义特征。用于衡量query和doc内容的语义相关性,一般利用词向量和深度学习模型产出,将词语、句子映射到某个向量空间,利用余弦相似度等方法计算特征分数。
- 意图特征。用于衡量query意图和doc内容整体的匹配程度,例如当query为百科查询类时,教育、人文历史类的doc更有可能满足要求。
- 负面特征。以上特征主要从query和doc相关的角度来设计,可以看做正面特征。而query中重要词语遗漏,紧密pair分散等情况并没有一个特征来体现,设计该特征的目的在于强化负面情况对排序的影响。
具体设计
假设query分词后的序列为$\left\{q_{1}, q_{2}, \ldots q_{n}\right\}$,doc标题分词后的序列为$\left\{t_{1}, t_{2} \cdots t_{m}\right\}$,正文序列为$\left\{c_{1}, c_{2} \cdots c_{k}\right\}$。
覆盖特征
简单地,可以统计query词在doc中命中个数(去重),假设为$h$,则有:
$$\begin{gather*} \text { cover_ratio }=\frac{h}{n} \end{gather*}$$其中$n$表示query中词语总数。额…好像有点太简单了吧。第一步优化,我们可以只关注query中的重要词,例如query=”开端的更新时间是什么”,那么“的”、“是”、“什么”这些词是否命中无关紧要,考虑它们的话反而会产生干扰。第二步优化,query匹配到doc中的词权重也不相同,对应上述query,假设一篇doc的标题是“开端电视剧周二周三更新”,另一篇文章的标题是“早睡是养成良好生活习惯的开端”,显然在同样匹配“开端”这个词的时候,前面的文章对应的权重应该更高一些。
第一步优化,我们需要获得query各个词的重要度,可通过词性、TF、IDF等进行判定。第二步优化,我们需要获得doc中的词权重。对于长度较短的标题,我们同样可以采用类似query的方法获得,此外还可以基于有监督的模型训练获得。对于正文中的词权重,简单地,可以使用TF-IDF,为了获得更好的效果可以利用深度模型进行计算,例如DeepCT模型。假设已获得query和doc词语的权重信息,那么覆盖度的计算公式为:
$$\begin{gather*} \text { cover_ratio }=\frac{\sum_{t \in{q_ {keywords}}} w_{t}^{d} \text {. is_cover }}{\sum_{t \in q_{k e y w o r d s}} w_{t}^{d}} \end{gather*}$$其中$q_{keywords}$表示query中的关键词,$is{cover}$表示doc中是否包含该词,$w_{t}^{d}$表示该词在doc中的权重。这里$\text { cover_ratio }$的含义是,对于query中所有关键词,对应其在doc中的权重,计算doc对其的覆盖情况。
命中特征
考虑query词在doc中命中的次数及权重来设计特征,比较简单的是TF-IDF算法,BM25算法是对TF-IDF算法的改进,应用更为广泛,公式如下:
$$\begin{gather*} f(q, d)=\sum_{w \in q \cap d} c(w, q) \frac{(k+1) c(w, d)}{c(w, d)+k\left(1-b+b \frac{|d|}{\text { avdl }}\right)} \log \frac{M+1}{d f(w)} \end{gather*}$$其中$b \in[0,1]$,$k_{1}, k_{3} \in[0,+\infty)$。以下描述中的顺序从左到右计算。
第一项$c(w,q)$,表示词语w在query中的词频;
第二项实质是对词语w词频的变换,$c(w,d)$表示词语w在文档d中的词频,通过公式的约束控制词频因子的上限,其上限为k+1,不会无线增长。例如当一个词语在文档中出现50次或100次时,都能说明该词与文本相关,但其相关性直观来说不应该是线性增长的,如下图所示:
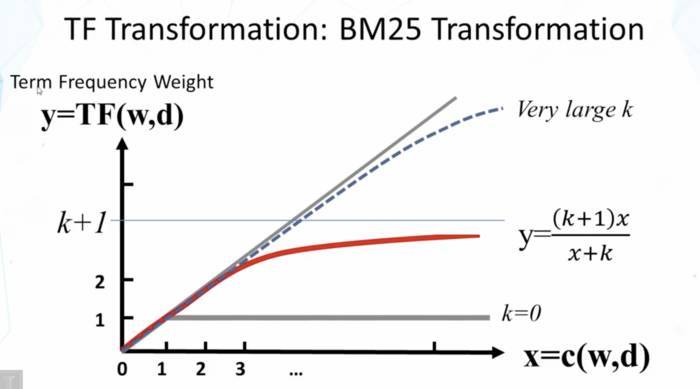
公式中分母k乘的系数目的是归一化文本长度。b表示[0,1]之间的常数,avdl表示文档的平均长度,对于文档d,如果其长度大于平均值,那么normalizer大于1,反之亦然。如下图所示:
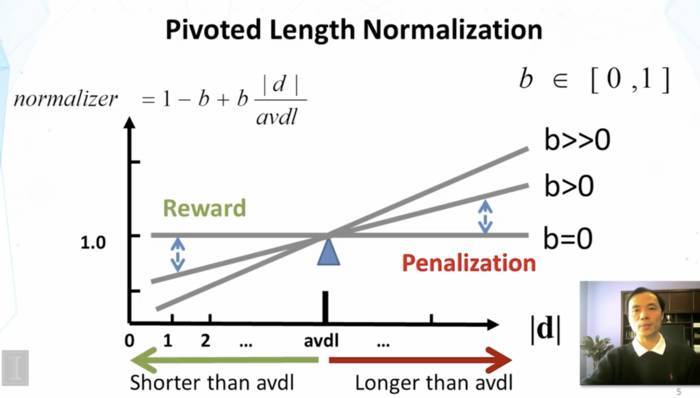
第三项表示词的逆文档频率,M表示所有文档数,$df(w)$表示包含该词的文档数。
紧密特征
关注query词语在doc中命中位置的分布,例如query=”上海中学”,$doc_1$的标题为“上海中学招生计划”,$doc_2$的标题为“上海有哪些比较好的中学”。query中的“上海”和“中学”紧密度较高,在$doc_1$和$doc_2$中都有命中,但在$doc_2$中分散命中,语义已发生了变化,显然$doc_1$与query更相关。为了进行区分,需要根据query词语的命中位置来设计紧密特征,具体有多种实现方法,这里大致介绍两种:
统计query词语整体分布情况。利用滑动窗口,统计每个窗口内的紧密度,最后取最大值。参考公式如下:$\begin{gather*}\text { proximity }_{1}=\max _{i \in { windows }}\left(\alpha_{w_i}^{\text {miss_ratio }} * \beta_{w_i}^{\text {reverse_ratio }}\right)\end{gather*}$,其中$windows$表示所有滑动窗口,$w_i$表示第i个窗口,$\alpha, \beta$为(0,1)区间的常数,$miss_ratio$表示窗口内未命中词语的比例,$reverse_ratio$表示窗口内逆序词语pair的比例。
统计query中紧密词语的命中情况。方法1的计算相对粗糙一些,query中重要性较低的词和非紧密词都可能对结果产生干扰。例如“的”、“啊”这些词语不命中其实无所谓。此外,非紧密词语不在一个窗口命中也可以,例如当query=”EDG、IG在哪年夺冠的”时,其中“EDG”与“IG”并无紧密关系,不能要求doc中两个词要紧密出现,假如某篇文章第一段介绍EDG夺冠,第二段介绍IG夺冠完全可以满足要求。因此进一步优化可以只考虑query中具有紧密关系词语之间的命中情况,参考公式如下:
$$\begin{gather*}\begin{array}{l} proximity_2=\frac{1} {total\_tightness}* \sum_{i \neq j} { tightness(t_{i},t_{j})}* \frac{1} {\operatorname{dist}\left(t_{i}, t_{j}\right)} \\ \operatorname{dist}\left(t_{i}, t_{j}\right)=\min _{i \neq j}\left(\phi\left(t_{i}, o\left(t_{j}\right)\right)\right)\\ \phi\left(t_{i}, t_{j}\right)=\left\{\begin{array}{l} \left|P_{t_{i,d}}-P_{t_{j ,d}}\right|, \text { if } P_{t_{j,d}}-P_{t_{i,d}}>0 \\ \left|P_{t_{i,d}}-P_{t_{j,d}}\right| * k, \text { if } P_{t_{j,d}}-P_{t_{i, d}}<0 \end{array}\right. \end{array} \end{gather*}$$其中$t_i,t_j$表示query中第i和第j个词语,$tightness(t_i,t_j)$表示两个词之间的紧密度,$dist(t_i,t_j)$表示两个词在doc中的距离,$o\left(t_{j}\right)$表示第j个词语在doc命中的集合,$P_{t_{i,d}}, P_{t_{j,d}}$表示query中第i个词语和第j个词语在doc的命中位置,$k$为某个常数。公式的含义是,对于query中每个紧密词pair,根据其紧密度和在doc中命中位置的距离计算紧密特征,由于词语在doc中可能存在多次命中,简单地,可以取pair命中位置的最短距离。此外,对于逆序命中的情况还要做一些惩罚,相应的增大距离。对于存在紧密pair的query,根据上述公式,如果在doc中命中位置越接近,则相应的分数越高,反之则越低。若query中不存在紧密pair,即total_tightness=0,那么可以给一个默认值,例如0。
权重特征
以key-value形式组织数据,例如对于学校、医院等实体名词,可根据经验、用户点击数据等离线计算好相应的权重,供在线生成特征。举个例子,当query=“北京大学”时,$doc_i$和$doc_j$中均命中了“北京大学”,但$doc_i$的内容是关于北京大学的招生简章,而$doc_j$则是关于北京大学财务处的信息,显然招生简章相比财务处是更为主要的需求。通过离线计算好的权重,我们可以给予$doc_i$更高的分数,使其排序更靠前。
语义特征
上述的覆盖、命中等特征属于传统的词法特征,会存在一些问题,例如:
- “电话”和“手机号”词义相近,与“电脑”词义较远,但只从字面进行匹配的话,两者的打分都是0,这显然不合理;
- 对于“上海到北京的机票价格”和“北京到上海的机票”两句话,当query=“北京到上海的机票多少钱“时,覆盖与命中特征的分数是一样的,但显然两句话的语义并不相同。
得益于大规模预训练语言模型和深度学习技术的发展,可以将query和doc表示为向量来计算语义相关性。
- 对于doc,一般来说将其拆分为标题和正文两个部分。标题通常较短,因此可以使用DSSM模型,例如ESIM来计算相关性。正文由于较长,可以将其分段后,离线生成各个段的向量表示,在线计算时根据命中段落中词的权重计算相关性。也可以离线提取关键句、关键段落等信息,用于在线计算;
- 将doc的标题和正文作为一个整体利用Transformer-XL、BERT-CNN或longformer等模型进行表示,然后计算其与query向量的相关性。但实践证明,虽然各个模型在长文建模方面进行了改进,但效果并不明显,相比于原始的BERT无明显提高,且最后得到的表示与起始的几个词语高度相关,后面词语对最终表示的影响很小。
实践中一般采取第一种方法,且由于正文内容较长,离线训练和在线计算使用资源较多,所以一般先获取query与title的语义相关特征,正文部分则在后续的优化中进行。
意图特征
上述的命中、紧密和语义等特征主要从词语、句子和段落粒度衡量query与doc的相关性,这里的意图特征关注query与doc整体内容的匹配情况。例如当query=”北冥鲲鹏”时,查询的目的大概率是了解相关的神话故事,那么从query侧可以将其分类为“百科查询”,doc侧教育、人文历史类的文章更有可能满足要求,而饮食、财经类的文章整体相关度较低。显然,为了获取意图匹配特征,需要进行query的意图识别和doc分类,query的意图识别需要在线完成,而doc分类可以离线计算好。值得注意的是,query的分类体系与doc的分类体系并不一定完全对应,因此需要学习两者之间的映射关系。例如上面举的例子,query意图为百科查询类时,对应的doc类型应是教育和人文历史类。这种映射关系的建立,简单地可以利用经验规则来制定,也可以根据点击数据、有监督的标注数据来学习。
负面特征
从衡量query和doc相关性的角度去设计特征,我们很自然的会关注两者相关的部分,进而设计出以上特征,这些可以看作正面特征。那么负面特征有哪些呢?常见的有:
- 缺失。query中存在重要词未命中;
- 分散。query中的紧密词语分散命中;
特征计算公式为:
$$\begin{gather*} \begin{array}{l} \text { neg_fea }=\sum_{i \in \text { non_stopwords }} \alpha * w_{i} \\ \alpha=\text { is_omit }+\text { scatter_degree } \end{array} \end{gather*}$$其中 non_stopwords表示query中的非停用词,$w_i$表示query中第i个词的权重,$\alpha$表示负面因子,$is_omit$表示该词语是否遗漏,$scatter_degree$表示分散系数,可根据词语之间的紧密度和命中情况归纳到几个区间。
特征分类
按照正面、负面以及内容粒度可以对以上特征进行如下分类:
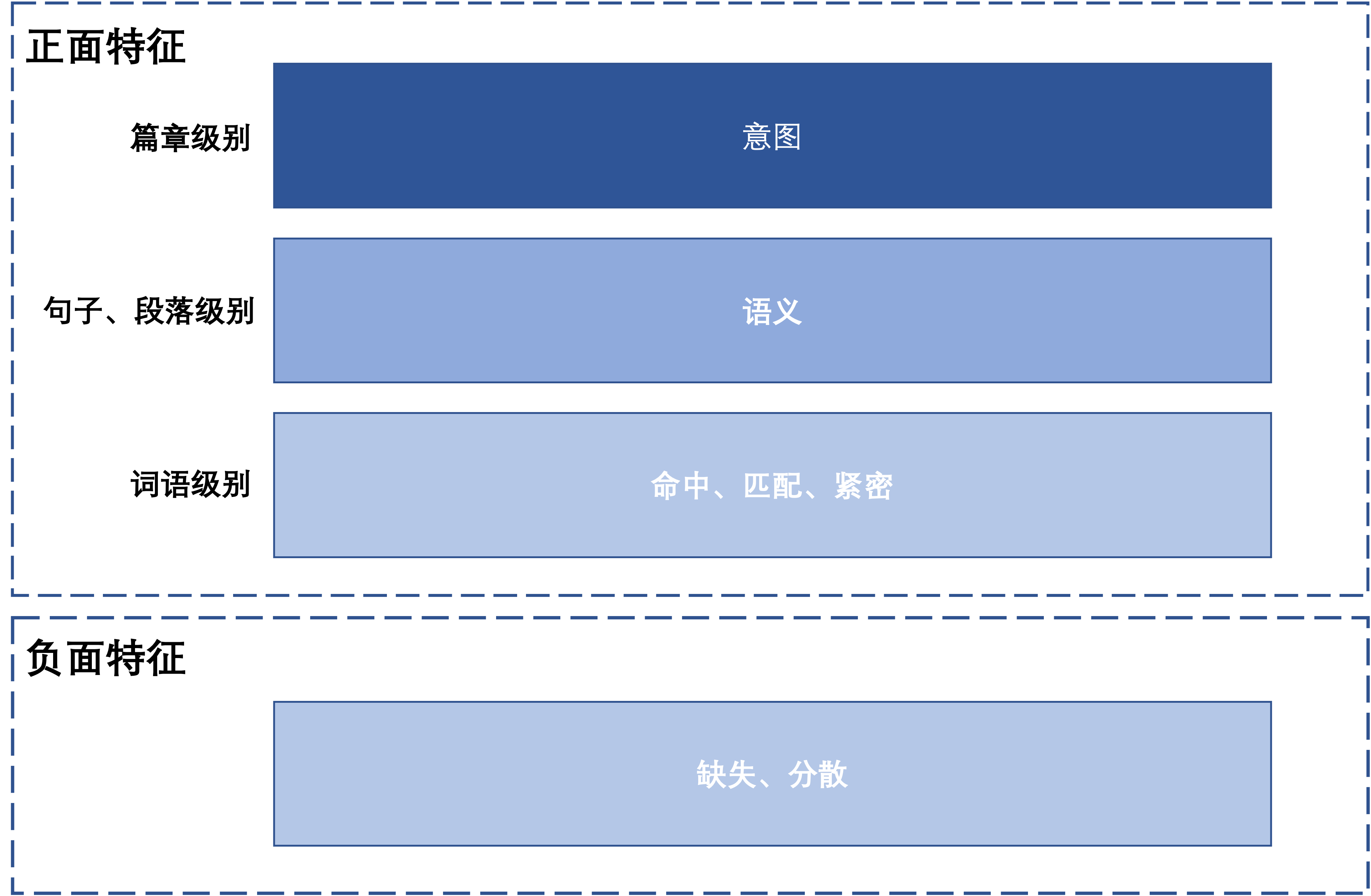
本文仅仅是讨论文本搜索特征设计的基本思路和方法,无论是特征的种类和计算方法都有很大的优化空间,抛砖引玉,抛砖引玉。
特征重要性
特征重要性的衡量方法一般有:
- 单独统计各个指标在标注数据集上的效果,例如只根据命中特征进行排序后结果中逆序的比例;
- 利用树模型,例如XGBoost进行训练,输出各个特征的重要性。
一般来说,以上各个特征的重要性排序为:语义特征>负面特征>覆盖特征>紧密特征>命中特征>意图特征。注意这只是在某个数据集上的测试结果,不一定适用于所有情况。